Fluid Mechanics and Hydraulic Machinery Miscellaneous
- A leaf is caught in a whirlpool. At a given instant, the leaf is at a distance of 120 m from the centre of the whirlpool. The whirlpool can be described by the following velocity distribution:
Vr = - 
60 × 103 
m/s and Vθ = 300 × 103 m/s 2πr 2πr
where r (in meters) is the distance from the centre of the whirlpool. What will be the distance of the leaf from the centre when it has moved through half a revolution?
-
View Hint View Answer Discuss in Forum
Radial distance = 120 m
Vr = - 60 × 103 m /s 2πr & Vθ = 300 × 103 m /s 2πr
& θ = πVr = -1 Vθ 5
we know thatVr = dr ...(i) dt & Vθ = rw = r dθ dt -5Vr = r dθ dt Vr = -r × dθ ...(ii) 5 dt
By equating (i) & (ii), we getdr = -r . dθ dt 5 dt
Integrating both sides, we get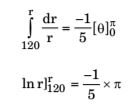
ln 
r 
= -π 120 5
By solving above, we get
r = 64 mCorrect Option: B
Radial distance = 120 m
Vr = - 60 × 103 m /s 2πr & Vθ = 300 × 103 m /s 2πr
& θ = πVr = -1 Vθ 5
we know thatVr = dr ...(i) dt & Vθ = rw = r dθ dt -5Vr = r dθ dt Vr = -r × dθ ...(ii) 5 dt
By equating (i) & (ii), we getdr = -r . dθ dt 5 dt
Integrating both sides, we get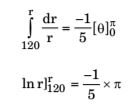
ln 
r 
= -π 120 5
By solving above, we get
r = 64 m
- In a steady flow through a nozzle, the flow velocity on the nozzle axis is given by v = u0 (1 + 3x/L)i, where x is the distance along the axis of the nozzle from its inlet plane and L is the length of the nozzle. The time required for a fluid particle on the axis to travel from the inlet to the exit plane of the nozzle is
-
View Hint View Answer Discuss in Forum

v = u0 
1 + 3x 
L ∴ dx = u0 
1 + 3x 
dt L ⇒ dx = dt u0 
1 + 3x 
L 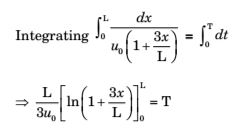
⇒ T = L ln(4) = L ln(4) 3u0 3u0
Correct Option: B

v = u0 
1 + 3x 
L ∴ dx = u0 
1 + 3x 
dt L ⇒ dx = dt u0 
1 + 3x 
L 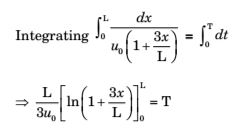
⇒ T = L ln(4) = L ln(4) 3u0 3u0
Direction: The gap between a moving circular plate and a stationary surface is being continuously reduced, as the circular plate comes down at a uniform speed V towards the stationary bottom surface, as shown in the figure. In the process, the fluid contained between the two plates flows out radially. The fluid is assumed to be incompressible and inviscid. 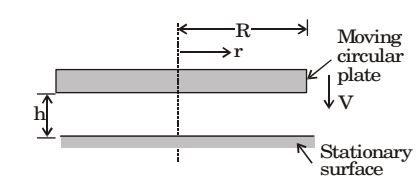
- The radial velocity Vr at any radius r, when the gap width is h, is
-
View Hint View Answer Discuss in Forum
V × πr² = Vr × 2πrh
Vr = Vr 2h
Correct Option: A
V × πr² = Vr × 2πrh
Vr = Vr 2h
- The radial component of the fluid acceleration at r = R is
-
View Hint View Answer Discuss in Forum
Radial acceleration
ar = Vr × ∂Vr + ∂Vr ∂r ∂t ar = V.r × ∂ 
V.r 
+ ∂ 
V.r 
2h ∂r 2h ∂t 2h -∂h = V ∂t ∴ ar = V.r × V.r + V.r × 
-1 ∂h 
2h 2h 2 h2 ∂t ∴ ar = V2r + 2V2r 4h2 4h2 ar = 3V2r 4h2
Correct Option: A
Radial acceleration
ar = Vr × ∂Vr + ∂Vr ∂r ∂t ar = V.r × ∂ 
V.r 
+ ∂ 
V.r 
2h ∂r 2h ∂t 2h -∂h = V ∂t ∴ ar = V.r × V.r + V.r × 
-1 ∂h 
2h 2h 2 h2 ∂t ∴ ar = V2r + 2V2r 4h2 4h2 ar = 3V2r 4h2
- Air flows at the rate of 1.5 m3/s through a horizontal pipe with a gradually reducing crosssection as shown in the figure. The two crosssections of the pipe have diameters of 400 mm and 200 mm. Take the air density as 1.2 kg/m3 and assume inviscid incompressible flow. The change in pressure (p2 – p1) (in kPa) between sections 1 and 2 is
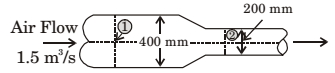
-
View Hint View Answer Discuss in Forum
P1 + V1² + Z1 = P2 + V2² + Z2 [Z = constant] δg 2g δg 2g A1 = π × 0.4² = 0.1256 m² 2 A2 = π × 0.2² = 0.314 m² 4 P2 − P1 = V1² − V2² δg 2g P2 − P1 = 1 
Q2 − Q2 
1.2 2 A1² A2² P2 − P1 = 0.6 × (1.5)² 
1 − 1 
A1² A2² P2 − P1 = 1.35 
1 − 1 
0.01577 0.00985
= 1.35 [63.41 – 1015.22]
= –1.28 ×10³ Pascal
= – 1.28 kPa
Correct Option: A
P1 + V1² + Z1 = P2 + V2² + Z2 [Z = constant] δg 2g δg 2g A1 = π × 0.4² = 0.1256 m² 2 A2 = π × 0.2² = 0.314 m² 4 P2 − P1 = V1² − V2² δg 2g P2 − P1 = 1 
Q2 − Q2 
1.2 2 A1² A2² P2 − P1 = 0.6 × (1.5)² 
1 − 1 
A1² A2² P2 − P1 = 1.35 
1 − 1 
0.01577 0.00985
= 1.35 [63.41 – 1015.22]
= –1.28 ×10³ Pascal
= – 1.28 kPa

