136. In a simple concentric shaft-bearing arrangement, the lubricant flows in the 2 mm gap between the shaft and the bearing. The flow may be assumed to be a plane Couette flow with zero pressure gradient. The diameter of the shaft is 100 mm and its tangential speed is 10 m/s. The dynamic viscosity of the lubricant is 0.1 kg/ms. The frictional resisting force (in Newton) per 100 mm length of the bearing is

1. 1. 15.707

   
   
   

   2. 15.706

   
   
   

   3. 15.708

   
   
   

   4. 15.709

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

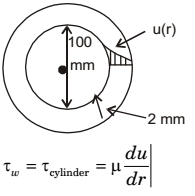
   F = A × μ	du	=	πDμ[ut - uw]
   	dr		(∆t)

   
   u_t = tangential velocity
   u_w = velocity at bearing
   

   F = π × 0.1 × 0.1 ×	0.1[10 - 0]
   	2 × 10-3

   
   F = 15.707 N.

   Correct Option: A

   
   

   F = A × μ	du	=	πDμ[ut - uw]
   	dr		(∆t)

   
   u_t = tangential velocity
   u_w = velocity at bearing
   

   F = π × 0.1 × 0.1 ×	0.1[10 - 0]
   	2 × 10-3

   
   F = 15.707 N.

---

137. For a fully developed flow of water in a pipe having diameter 10 cm, velocity 0.1 m/s and kinematic viscosity 10–5 m²/s, the value of Darcy friction factor is ________.

1. 1. 0.364

   
   
   

   2. 0.264

   
   
   

   3. 0.064

   
   
   

   4. 0.164

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given, D = 10 cm = 0.1 m
   V = 0.1 m/s
   v = 10^–5 m² /s
   

   Re =	VD	=	0.1 × 0.1
   	v		10-5

   
   

   Darcy friction factor =	64	(for laminar flow)
   	Re

   
   

   =	64	= 0.064
   	1000

   Correct Option: C

   Given, D = 10 cm = 0.1 m
   V = 0.1 m/s
   v = 10^–5 m² /s
   

   Re =	VD	=	0.1 × 0.1
   	v		10-5

   
   

   Darcy friction factor =	64	(for laminar flow)
   	Re

   
   

   =	64	= 0.064
   	1000

---

---

138. Water flows through a pipe having an inner radius of 10 mm at the rate of 36 kg/hr at 25°C. The viscosity of water at 25°C is 0.001 kg/ms. The Reynolds number of the flow is ______.

1. 1. 0.1

   
   
   

   2. 0.2

   
   
   

   3. 0.3

   
   
   

   4. 0.4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Re =	ρVD	........(i)
   	μ

   
   From continuity equation :-
   ṁ = ρAV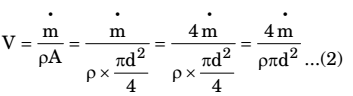
   
   put (2) in (1), we get
   

   Correct Option: A

   Re =	ρVD	........(i)
   	μ

   
   From continuity equation :-
   ṁ = ρAV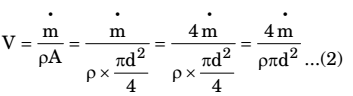
   
   put (2) in (1), we get
   

---

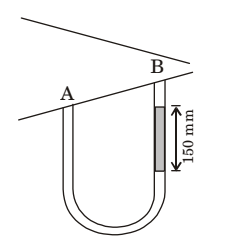
139. A U-tube manometer with a small quantity of mercury is used to measure the static pressure difference between two locations A and B in a conical section through which an in compressible fluid flows. At a particular flow rate, the mercury column appears as shown in the figure. The density of mercury is 13600 kg/ m³ and g - 9.81 m/s². Which of the following is correct?
     

1. 1. Flow direction is A to B and P_A – P_B = 20 kPa

   
   
   

   2. Flow direction is B to A and P_A – P_B = 1.4 kPa

   
   
   

   3. Flow direction is A to B and P_B – P_A = 20 kPa

   
   
   

   4. Flow direction is B to A and P_B – P_A = 1.4 kPa

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   PA – PB = rg. Dh
   = 13600 × 9.81 × .15
   = 20 kPa
   As pressure is decreasing from A to B, so flow direction is A to B.

   Correct Option: A

   
   PA – PB = rg. Dh
   = 13600 × 9.81 × .15
   = 20 kPa
   As pressure is decreasing from A to B, so flow direction is A to B.

---

---

140. A venturimeter of 20 mm throat diameter is used to measure the velocity of water in a horizontal pipe of 40 mm diameter. If the pressure difference between the pipe and throat sections is found to be 30 kPa then, neglecting frictional losses, the flow velocity is

1. 1. 0.2 m/s

   
   
   

   2. 1.0 m/s

   
   
   

   3. 1.4 m/s

   
   
   

   4. 2.0 m/s

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know, A₁ V₁ = A₂ V₂
   

   ƥ V2 =	D21	V1 =	16	V1
   	D22		4

   
   ∴ V₂ = 4V₁
   Applying Bernoulli's Equation
   

   	p1	+	v21	+ z1 =	p2	+	p22	+ z2
   	ρg		2g		ρg		2g

   
   

   	P1 - P2	=	V22 - V21
   	eg		2g

   
   

   ƥ	15V21	=	30 × 103
   	2		1000

   
   ƥ V²₁ = 4
   ƥ V₁ = 2.0 m/s
   So velocity of flow is 2.0 m/sec

   Correct Option: D

   We know, A₁ V₁ = A₂ V₂
   

   ƥ V2 =	D21	V1 =	16	V1
   	D22		4

   
   ∴ V₂ = 4V₁
   Applying Bernoulli's Equation
   

   	p1	+	v21	+ z1 =	p2	+	p22	+ z2
   	ρg		2g		ρg		2g

   
   

   	P1 - P2	=	V22 - V21
   	eg		2g

   
   

   ƥ	15V21	=	30 × 103
   	2		1000

   
   ƥ V²₁ = 4
   ƥ V₁ = 2.0 m/s
   So velocity of flow is 2.0 m/sec

---