101. For a certain two-dimensional incompressible flow, velocity field is given by 2xyi – y² j. The streamlines for this flow are given by the family of curves

1. 1. x²y² = constant

   
   
   

   2. xy² = constant

   
   
   

   3. 2xy – y² = constant

   
   
   

   4. xy – constant

   
   
   

---

1. View Hint View Answer Discuss in Forum

   v = 2xy i – y²j
   

   u =		δx	, v = -	δx
   		δy		δx

   
   

   2xy =	δx	= 2
   	δy

   
   2xyδy = δψ
   on integrating
   ψ = xy² + f(x)
   = y¹ + f'(x)
   f'(x) = 0
   ⇒ f(x)= constant
   so ψ= xy² + constant

   Correct Option: B

   v = 2xy i – y²j
   

   u =		δx	, v = -	δx
   		δy		δx

   
   

   2xy =	δx	= 2
   	δy

   
   2xyδy = δψ
   on integrating
   ψ = xy² + f(x)
   = y¹ + f'(x)
   f'(x) = 0
   ⇒ f(x)= constant
   so ψ= xy² + constant

---

102. The volumetric flow rate (per unit depth) between two streamlines having stream function ψ1 and ψ2 is

1. 1. |ψ₁ + ψ₂|

   
   
   

   2. ψ₁ ψ₃

   
   
   

   3. ψ₁ /ψ₂

   
   
   

   4. |ψ₁ – ψ₂|

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: D

   NA

---

---

103. The velocity field of an incompressible flow is given by V = (a₁x + a₂y + a₃ z)i + (b₁x + b₂y + b₃ z)j + (c₁x + c₂y + c₃ z)k, where a₁ = 2 and c₃ = –4. The value of b₂ is _________.

1. 1. 2

   
   
   

   2. 1

   
   
   

   3. 3

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   		δu	+	δv	+	δw	= 0
   		δx		δy		δz

   
   a₁ + b₂ + c₃ = 0
   2 – 4 + b₂ = 0
   b₂ = 2
   

   Correct Option: A

   		δu	+	δv	+	δw	= 0
   		δx		δy		δz

   
   a₁ + b₂ + c₃ = 0
   2 – 4 + b₂ = 0
   b₂ = 2
   

---

104. If the fluid velocity for a potential flow is given by V(x, y) = u(x, y)i + v(x, y)j with usual notations, then the slope of the potential line at (x, y) is

1. 1. 	v
      	u

   
   
   

   2. -	u²
      	v

   
   
   

   3. -	v
      	u²

   
   
   

   4. 	u
      	v

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Here V(x, y) = u(x, y) i + v(x, y) j
   

   As we know that u =	-δφ
   	δx

   
   

   ∴	-δφ	= -v(x,y) ....(i)
   	δx

   
   

   Similarly v =	-δφ
   	δy

   
   

   ∴	-δφ	= -v(x,y) ....(ii)
   	δy

   
   From equations (i) and (ii) we get,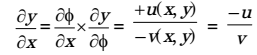
   
   

   Correct Option: B

   Here V(x, y) = u(x, y) i + v(x, y) j
   

   As we know that u =	-δφ
   	δx

   
   

   ∴	-δφ	= -v(x,y) ....(i)
   	δx

   
   

   Similarly v =	-δφ
   	δy

   
   

   ∴	-δφ	= -v(x,y) ....(ii)
   	δy

   
   From equations (i) and (ii) we get,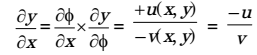
   
   

---

---

105. Consider a velocity field V K(yi + xk), where K is a constant. The vorticity, Ω Z, is
     

1. 1. –K

   
   
   

   2. K

   
   
   

   3. –K/2

   
   
   

   4. K/2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: A

   NA

---