156. A circular plate 1 m in diameter is submerged vertically in water such its upper edge is 8 m below the free surface of water. The total hydro static pressure force on one side of plate is

1. 1. 6.7 kN

   
   
   

   2. 65.4 kN

   
   
   

   3. 45.0 kN

   
   
   

   4. 77.0 kN

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

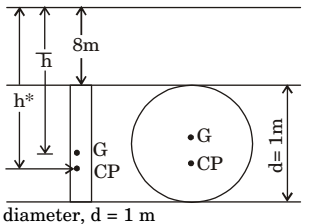
   h = 8 +	d
   	2

   
   

   = 8 +	d	= 8.5 m
   	2

   
   Surface area,
   

   A =	π	d2 =	3.14	× 12 = 0.785 m2
   	4		4

   
   Total hydrostatic pressure force, F = ρghA
   F = 1000 × 9.81 × 8.5 × 0.785 = 65458 N
   or F = 65.45 KN

   Correct Option: B

   
   

   h = 8 +	d
   	2

   
   

   = 8 +	d	= 8.5 m
   	2

   
   Surface area,
   

   A =	π	d2 =	3.14	× 12 = 0.785 m2
   	4		4

   
   Total hydrostatic pressure force, F = ρghA
   F = 1000 × 9.81 × 8.5 × 0.785 = 65458 N
   or F = 65.45 KN

---

157. Kinematic viscosity of air at 20°C is given to be 1.6 × 10^-5 m²/s. Its kinematic viscosity at 70°C will be varying approximately

1. 1. 2.2 × 10^-5 m²/s

   
   
   

   2. 1.6 × 10^-5 m²/s

   
   
   

   3. 1.2 × 10^-5 m²/s

   
   
   

   4. 3.2 × 10^-5 m²/s

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Viscosity of gas increases with increasing temperature.

   Correct Option: A

   Viscosity of gas increases with increasing temperature.

---

---

158. Assuming constant temperature condition and air to be an ideal gas, the variation in atmospheric pressure with height calculated from fluid statics is

1. 1. linear

   
   
   

   2. exponential

   
   
   

   3. quadratic

   
   
   

   4. cubic

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: B

   NA

---

159. For a Newtonian fluid

1. 1. shear stress is proportional to shear strain

   
   
   

   2. rate of shear stress is proportional to shear strain

   
   
   

   3. shear stress is proportional to rate of shear strain

   
   
   

   4. rate of shear stress is proportional to rate of shear strain

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For a Newtonian fluid, shear stress is proportional to rate of shear strain.

   Correct Option: C

   For a Newtonian fluid, shear stress is proportional to rate of shear strain.

---

---

160. Kaplan water turbine is commonly used when the flow through its runner is

1. 1. axial and the head available is more than 100 m

   
   
   

   2. axial and the head available is less than 10 m

   
   
   

   3. radial and the head available is more than 100 m

   
   
   

   4. mixed and the head available is about 50 m

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Kaplan turbine is an axial flow turbine and works at low heads (<50).

   Correct Option: B

   Kaplan turbine is an axial flow turbine and works at low heads (<50).

---