Fluid Mechanics and Hydraulic Machinery Miscellaneous
- Air flows through a venturi and into atmosphere. Air density is ρa; atmospheric pressure is ρa; throat diameter is Dt; exit diameter is D and exit velocity is U. The throat is connected to a cylinder containing a friction less piston attached to a spring. The spring constant is k. The bottom surface of the piston is exposed to atmosphere. Due to the flow, the piston moves by distance x. Assuming in compressible friction less flow, x is
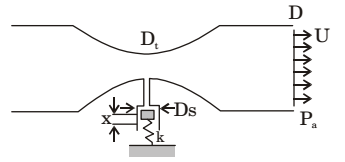
-
View Hint View Answer Discuss in Forum
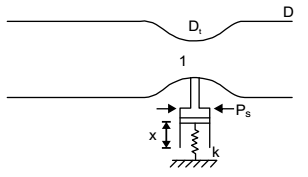
Applying Bernoulli’s equation at points (1) and (2), we havep1 + v21 + z1 = p2 + p22 + z2 ρg 2g ρg 2g
Since venturi is horizontal
z1 = z2Now p1 - p2 = v22 - p21 ρg ρg 2g 2g ⇒(p1 - p2) = ρg (v22 - v21) = ρ = (v22 - v21) 2g g
Since P2 = Pa = atmospheric pressure∴ (P2 - Pa) ρ (v22 - v21) ........(i) 2
Applying continuity equation at points (i) and (ii), we have
A1 v1 = A2 v2⇒ v1 = 
A2 
v2 since V2 = U A1 
v1 = 
D 
2 U Dt
From equation (i),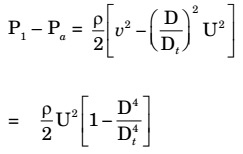
At point P
Spring force = pressure force due air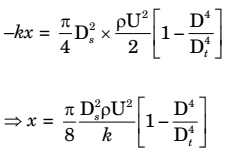
Correct Option: D

Applying Bernoulli’s equation at points (1) and (2), we havep1 + v21 + z1 = p2 + p22 + z2 ρg 2g ρg 2g
Since venturi is horizontal
z1 = z2Now p1 - p2 = v22 - p21 ρg ρg 2g 2g ⇒(p1 - p2) = ρg (v22 - v21) = ρ = (v22 - v21) 2g g
Since P2 = Pa = atmospheric pressure∴ (P2 - Pa) ρ (v22 - v21) ........(i) 2
Applying continuity equation at points (i) and (ii), we have
A1 v1 = A2 v2⇒ v1 = 
A2 
v2 since V2 = U A1 
v1 = 
D 
2 U Dt
From equation (i),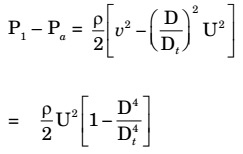
At point P
Spring force = pressure force due air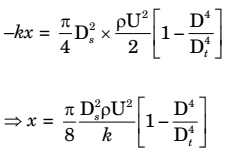
- Water flows though a vertical contraction from a pipe of diameter d to another of diameter d/2 (see fig.) The flow velocity at the inlet to the contraction is 2 m/s and pressure 200 kN/m2. If the height of the contraction measures 2m,then pressure at the exit of the contraction will be very nearly

-
View Hint View Answer Discuss in Forum
From continuity equation,
A1 v1 = A2 v2or π × d2 × 2 = π 
d 
2 × v2 4 4 2
or v2 = 8 m/s.
Applying Bernoulli's theorem,p1 + v21 + z1 = p2 + p22 + z2 w 2g w 2g or 200 × 1000 + (2)2 + 0 9810 2 × 9.81 or p2 + (8)2 + 2 w 2 × 9.81
or p2 =150.38 kN/m2Correct Option: C
From continuity equation,
A1 v1 = A2 v2or π × d2 × 2 = π 
d 
2 × v2 4 4 2
or v2 = 8 m/s.
Applying Bernoulli's theorem,p1 + v21 + z1 = p2 + p22 + z2 w 2g w 2g or 200 × 1000 + (2)2 + 0 9810 2 × 9.81 or p2 + (8)2 + 2 w 2 × 9.81
or p2 =150.38 kN/m2
- In a venturimeter, the angle of the diverging section is more than that of converging section. State: (T/F)
-
View Hint View Answer Discuss in Forum
False
Correct Option: A
False
- In a Lagrangian system, the position of a fluid particle in a flow is described as x = x0e–kt and y = y0ekt where t is the time while x0, y0, and k are constants. The flow is
-
View Hint View Answer Discuss in Forum
x direction scalar of velocity field,
u = dx dt
u = - kx0e-kt
y direction scalar of velocity fieldv = dy dt
v = ky0ekt
v̄ = uî + vĵ
V̄ = - kx0e-ktî + ky0ektĵ
u & v are non zero scalar t ≥ 0 so it is 2D flow. 2D possible flow fieldδu + δv = 0 δx δy δ (- kx0e-kt) + δ (ky0ekt) = 0 δx δy
0 + 0 = 0 continuity satisfied.δu + k2x0e-kt δt δv + k2y0ekt δt δu ≠ 0 δt δv ≠ 0 δt
So, flow is unsteady.Correct Option: B
x direction scalar of velocity field,
u = dx dt
u = - kx0e-kt
y direction scalar of velocity fieldv = dy dt
v = ky0ekt
v̄ = uî + vĵ
V̄ = - kx0e-ktî + ky0ektĵ
u & v are non zero scalar t ≥ 0 so it is 2D flow. 2D possible flow fieldδu + δv = 0 δx δy δ (- kx0e-kt) + δ (ky0ekt) = 0 δx δy
0 + 0 = 0 continuity satisfied.δu + k2x0e-kt δt δv + k2y0ekt δt δu ≠ 0 δt δv ≠ 0 δt
So, flow is unsteady.
- For a two-dimensional in compressible flow field given by ū = A(x̂ i – yĵ), where A > 0, which one of the following statements is FALSE?
A. It satisfies continuity equation
B. It is unidirectional when x → 0 and y → ∞.
C. Its streamlines are given by x = y.
D. It is irrotational
-
View Hint View Answer Discuss in Forum
C is the false statement
2D in compressible flow continuity equation.δu + δv = 0 δx δy δ(Ax) + δ(- Ay) = 0 δx δy
A – A = 0 it satisfies continuity equation.
⇒ As V̄ = Ax î - Ayĵ
As y → ∞ velocity vector field will not be defined along y axis.
So flow will be along x-axis i.e. 1-D flow.
⇒ Stream line equation for 2Ddx = dy u v dx = dy Ax - Ay
In x = – ln y + ln c
ln xy = ln c
xy = c → streamline equationCorrect Option: C
C is the false statement
2D in compressible flow continuity equation.δu + δv = 0 δx δy δ(Ax) + δ(- Ay) = 0 δx δy
A – A = 0 it satisfies continuity equation.
⇒ As V̄ = Ax î - Ayĵ
As y → ∞ velocity vector field will not be defined along y axis.
So flow will be along x-axis i.e. 1-D flow.
⇒ Stream line equation for 2Ddx = dy u v dx = dy Ax - Ay
In x = – ln y + ln c
ln xy = ln c
xy = c → streamline equation

