1. Velocity vector of a flow field is given as = 2xyî - x²zĵ. The vorticity vector at (1, 1, 1) is

1. 1. 4î - ĵ

   
   
   

   2. 4î - k̂

   
   
   

   3. î - 4ĵ

   
   
   

   4. î - 4k̂

   
   
   

---

1. View Hint View Answer Discuss in Forum

   v = 2xyi – x 2zj
   Velocity of a vector = ∇ × v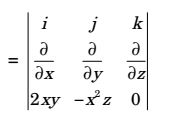
   
   

   = î

   0 -

   δ

   ( - x²z)

   - î

   0 -

   δ

   (2xy)

   - k̂

   0 -

   δ

   (-x²z) -

   δ

   (2xy)

   δz

   δz

   δx

   δy

   
   = î(-x²) + k̂(-2 × z - 2X)
   At(1 , 1 , 1),
   ∇ × v = î + k̂ (-2 -2) = i - 4k

   Correct Option: D

   v = 2xyi – x 2zj
   Velocity of a vector = ∇ × v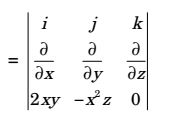
   
   

   = î

   0 -

   δ

   ( - x²z)

   - î

   0 -

   δ

   (2xy)

   - k̂

   0 -

   δ

   (-x²z) -

   δ

   (2xy)

   δz

   δz

   δx

   δy

   
   = î(-x²) + k̂(-2 × z - 2X)
   At(1 , 1 , 1),
   ∇ × v = î + k̂ (-2 -2) = i - 4k

---

2. A Prandtl tube (Pitot-static tube with C = 1) is used to measure the velocity of water. The differential manometer reading is 10 mm of liquid coiumn with a relative density of 10. Assuming g = 9.8 m/s², the velocity of water (in m/s) is _____ .

1. 1. 2. 8 m/ s

   
   
   

   2. 2 m/ s

   
   
   

   3. 1.328 m/ s

   
   
   

   4. 1.25m/ s

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Velocity as water = C_v √2gh
   C_v = 1 (Given)
   

   h = x		sg	- 1
   		s0

   
   = 0.01 (10 – 1) = 0.09 m
   ∴ velocity of flow = √2 × 9.8 × 0.09 = 1.328 m/ s

   Correct Option: C

   Velocity as water = C_v √2gh
   C_v = 1 (Given)
   

   h = x		sg	- 1
   		s0

   
   = 0.01 (10 – 1) = 0.09 m
   ∴ velocity of flow = √2 × 9.8 × 0.09 = 1.328 m/ s

---

---

3. A streamline and an equipotential line in a flow field

1. 1. are parallel to each other

   
   
   

   2. are perpendicular to each other

   
   
   

   3. intersect at an acute angle

   
   
   

   4. are identical

   
   
   

---

1. View Hint View Answer Discuss in Forum

   	dy			×		dy			= - 1
   	dx		φ			dx		ψ

   
   Slope of equipotential Line × slope of stream function = – 1
   They are orthogonal to each other.

   Correct Option: B

   	dy			×		dy			= - 1
   	dx		φ			dx		ψ

   
   Slope of equipotential Line × slope of stream function = – 1
   They are orthogonal to each other.

---

4. The arrangement shown in the figure measures the velocity V of a gas of density 1 kg/m³ flowing through a pipe. The acceleration due to gravity is 9.81 m/s². If the manometric fluid is water (density 1000 kg/m³) and the velocity V is 20 m/ s, the differential head h(in mm) between the two arms of the manometer is _________.
   

1. 1. h = 30.31 mm of water

   
   
   

   2. h = 10.12 mm of water

   
   
   

   3. h = 14.38 mm of water

   
   
   

   4. h = 20.38 mm of water

   
   
   

---

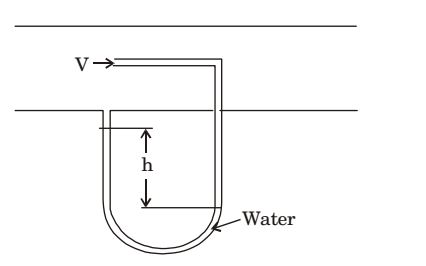
1. View Hint View Answer Discuss in Forum

   Dynamic pressure of gas = (δgh)_water
   

   1	δgasv2 = δm × 9.81 × h
   2

   
   

   1	× 1 × (20)² = 1000 × 9.81 × h
   2

   
   h = 0.02038 m of water
   h = 20.38 mm of water

   Correct Option: D

   Dynamic pressure of gas = (δgh)_water
   

   1	δgasv2 = δm × 9.81 × h
   2

   
   

   1	× 1 × (20)² = 1000 × 9.81 × h
   2

   
   h = 0.02038 m of water
   h = 20.38 mm of water

---

---

5. The Newtonian fluid has the following velocity field:
   = x²yî + 2xy²ĵ - yz³k̂
   The rate shear deformation ε_yz at the point x = –2, y = –1 and z = 2 for the given flow is

1. 1. –6

   
   
   

   2. –2

   
   
   

   3. –12

   
   
   

   4. 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   V = x⊃î + 2xy²zĵ - yz²̂k
   Shear strain
   

   yz =	1		δv	+	δw		=	1	(2xy² - z³)
   	2		δz		δy			2

   
   at (–2π, 2), we get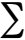
   

   yz =	1	(- 4 - 8)) = - 6
   	2

   Correct Option: A

   V = x⊃î + 2xy²zĵ - yz²̂k
   Shear strain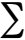
   

   yz =	1		δv	+	δw		=	1	(2xy² - z³)
   	2		δz		δy			2

   
   at (–2π, 2), we get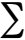
   

   yz =	1	(- 4 - 8)) = - 6
   	2

---