61. The ratio	PA − PB	.
    	(1/2)ρu0²

    
    (where p_A and p_B are the pressures at section A and B, respectively, and ρ is the density of the fluid), is

1. 1. 1

      [1 + (δ/H)]²

   
   
   

   2. 1

      [1 − (δ/H)]²

   
   
   

   3. 1

      [1 − (2δ/H)]²

   
   
   

   4. 1

      1 + (δ/H)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Applying Bernoulli’s equation at sections A and B, we get
   

   PA	+	u0²	+ ZA =	PA	+	Vm²	+ ZB
   ρg		2g		ρg		2g

   
   

   PA	+	u0²	=	PB	+	Vm²
   ρg		2g		ρg		2g

   or	PA	+	PB	=	Vm²	+	u0²
   	Pg		ρg		2g		2g

   
   Now, the ratio
   

   PA − PB/(1/2)ρ0² =	ρVm²	−	ρu0²
   	2		2
   	1	ρu0²
   	2

   
   

   =	Vm² − u0²	=		Vm		²	− 1
   	u0²			u0

   
   

   Substituting the Value of	Vm	=	1
   	u0		1 − (δ/H)

   
   we get
   

   PA − PB	=	1	− 1
   (1/2)ρ0²		[1 − (δ/H)]²

   Correct Option: B

   Applying Bernoulli’s equation at sections A and B, we get
   

   PA	+	u0²	+ ZA =	PA	+	Vm²	+ ZB
   ρg		2g		ρg		2g

   
   

   PA	+	u0²	=	PB	+	Vm²
   ρg		2g		ρg		2g

   or	PA	+	PB	=	Vm²	+	u0²
   	Pg		ρg		2g		2g

   
   Now, the ratio
   

   PA − PB/(1/2)ρ0² =	ρVm²	−	ρu0²
   	2		2
   	1	ρu0²
   	2

   
   

   =	Vm² − u0²	=		Vm		²	− 1
   	u0²			u0

   
   

   Substituting the Value of	Vm	=	1
   	u0		1 − (δ/H)

   
   we get
   

   PA − PB	=	1	− 1
   (1/2)ρ0²		[1 − (δ/H)]²

---

62. The dimension of surface tension is

1. 1. ML^–1

   
   
   

   2. L² T^–1

   
   
   

   3. ML^–1 T^–1

   
   
   

   4. MT^–2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Surface tension (σ)
   

   σ =	F	=	N	=	kg − m	= MT−2
   	L		m		s2 × m

   Correct Option: D

   Surface tension (σ)
   

   σ =	F	=	N	=	kg − m	= MT−2
   	L		m		s2 × m

---

---

63. If P is the gauge pressure within a spherical droplet, then gauge pressure within a bubble of the same fluid and of same size will be

1. 1. P/4

   
   
   

   2. P/2

   
   
   

   3. P

   
   
   

   4. 2P

   
   
   

---

1. View Hint View Answer Discuss in Forum

   P = Gauge pressure within a spherical droplet
   

   Pdroplet =	4σ	for droplet
   	d

   
   

   Pbubble =	8σ	for bubble
   	d

   
   P_bubble = 2 P_droplet

   Correct Option: D

   P = Gauge pressure within a spherical droplet
   

   Pdroplet =	4σ	for droplet
   	d

   
   

   Pbubble =	8σ	for bubble
   	d

   
   P_bubble = 2 P_droplet

---

64. The pressure gauges G_{1 and G2 installed on the system show pressure of ρG1 = 5.00 bar and ρG2 = 1.00 bar. The value of unknown pressure P is [Atmospheric pressure = 1.01 bar]}
    

1. 1. 1.01 bar

   
   
   

   2. 2.01 bar

   
   
   

   3. 5.00 bar

   
   
   

   4. 7.01 bar

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
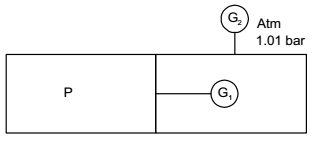
   P = P_G1 + P_G2 + P_atm
   P = 5 + 1 + 1.01 = 7.01 bar

   Correct Option: D

   
   P = P_G1 + P_G2 + P_atm
   P = 5 + 1 + 1.01 = 7.01 bar

---

---

65. Oil in a hydraulic cylinder is compressed from an initial volume 2 m³ to 1.96 m³. If the pressure of oil in the cylinder changes from 40 MPa to 80 MPa during compression, the bulk modulus of elasticity of oil is

1. 1. 1000 MPa

   
   
   

   2. 2000 MPa

   
   
   

   3. 4000 MPa

   
   
   

   4. 8000 MPa

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Bulk modules of elasticity, 1 dh K =	−dh
   	dv/V1

   
   

   K = −V1	−dp
   	dv

   
   

   K =	−2 × 40
   	−0.04

   
   K = 2000 MPa

   Correct Option: B

   Bulk modules of elasticity, 1 dh K =	−dh
   	dv/V1

   
   

   K = −V1	−dp
   	dv

   
   

   K =	−2 × 40
   	−0.04

   
   K = 2000 MPa

---