Fluid Mechanics and Hydraulic Machinery Miscellaneous Easy Questions and Answers

Fluid Mechanics and Hydraulic Machinery Miscellaneous

The aerodynamic drag on a sports car depends on its shape. The car has a drag coefficient of 0.1 with the windows and the roof closed. With t he windows and t he r oof open, t he dr ag coefficient becomes 0.8. The car travels at 44 km/h with the windows and roof closed. For the same amount of power needed to overcome the aerodynamic drag, the speed of the car with the windows and roof open (round off to two decimal places), is ____ km/h. (The density of air and the frontal area may be assumed to be constant.

The velocity profile inside the boundary layer for flow over a plate is given as (u / u_∞) = sin{(π/2)(y/δ)} , where U_∞ is the free stream velocity and δ is the local boundary layer thickness. If δ* is the local displacement thickness, the value of (δ* / δ) is

A steady laminar boundary layer Is formed over a flate plate as shown in the figure, The free stream velocity of the fluid is U0. The velocity profile at the inlet a-b is unlform, while that at a downstream location c–d is given by

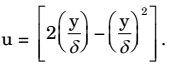
The ratio of the mass flow rate, m _bd leaving through the horizontal section b-d to that entering through the vertical section a-b is ____

An incompressible fluid flows over a flat plate with zero pressure gradient. The boundary layer thickness is 1 mm at a location where the Reynolds number is 1000. If the velocity of the fluid alone is increased by a factor of 4, then the boundary layer thickness at the same location, in mm will be

Consider an incompressible laminar boundary layer flow over a flat plate of length L, aligned with the direction of an incoming uniform free stream. If F is the ratio of the drag force on the front half of the plate to the drag force on the rear half, then

Boundary layer thickness, δ ∝	1
	√Re

Re ∝ V ⇒ δ ∝	1
	√V

Boundary layer thickness, δ ∝	1
	√Re

Re ∝ V ⇒ δ ∝	1
	√V