Fluid Mechanics and Hydraulic Machinery Miscellaneous
- The maximum velocity of a one-dimensional incompressible fully developed viscous flow, between two fixed parallel plates, is 6 ms-1. The mean velocity (in ms-1) of the flow is
-
View Hint View Answer Discuss in Forum
For fully developed incompressible viscous flow,
Vmean = 2 Vmax 3 = 2 × 6 = 4 m/s 3 Correct Option: C
For fully developed incompressible viscous flow,
Vmean = 2 Vmax 3 = 2 × 6 = 4 m/s 3
- The pressure drop for laminar flow of a liquid in a smooth pipe at normal temperature and pressure is
-
View Hint View Answer Discuss in Forum
∆ P = 32μUL D²
Above equation shows that ∆P is independent of velocity.Correct Option: C
∆ P = 32μUL D²
Above equation shows that ∆P is independent of velocity.
- The velocity profile of a fully developed laminar flow in a straight circular pipe, as shown in the figure, is given by the expression
u(r) = − R² 
∂p 

1 − r² 
4μ ∂x R²
where ∂p/∂x is a constant
The average velocity of fluid in the pipe is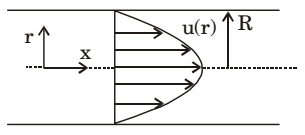
-
View Hint View Answer Discuss in Forum
u = − R² 
− dp 

1 − r² 
4μ dx R
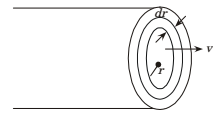
dQ =u (2πrdr)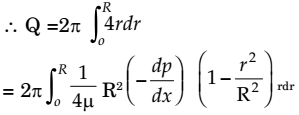
Solving, we getQ = − πR² 
− dp 
8μ dx
Now Q = Area ´ average velocity∴ uav = Q = Q Area πR2 or uav = R² 
dp 
8μ dx Correct Option: A

u = − R² 
− dp 

1 − r² 
4μ dx R
dQ =u (2πrdr)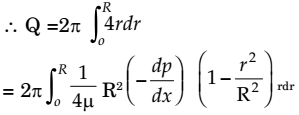
Solving, we getQ = − πR² 
− dp 
8μ dx
Now Q = Area ´ average velocity∴ uav = Q = Q Area πR2 or uav = R² 
dp 
8μ dx
- Two pipes of uniform section but different diameters carry water at the same flow rate. Water properties are the same in the two pipes. The Reynolds number, based on the pipe diameter
-
View Hint View Answer Discuss in Forum
Reynolds number, Re = Vd υ Discharge, Q = AV = π d2V 4 From above, = 4Q πd2 ∴ Reynolds No. = 4Q × d πd2 2 Reynolds No. = 4Q ....(1) πd From (1), Re ∝ 1 2
Reynolds number is large in the Narrow pipe.Correct Option: B
Reynolds number, Re = Vd υ Discharge, Q = AV = π d2V 4 From above, = 4Q πd2 ∴ Reynolds No. = 4Q × d πd2 2 Reynolds No. = 4Q ....(1) πd From (1), Re ∝ 1 2
Reynolds number is large in the Narrow pipe.
Direction: Consider a linear programming problem with two variable and two constraints. The objective function is maximize x1 + x2. The corner points of the feasible region are (0, 0), (0,2) (2, 0) and (4/3, 4/3)
- Oil is being pumped through a straight pipe, the pipe length, diameter and volumetric flow rate are all doubled in a new arrangement. The pipe friction factor, however, remains constant. The ratio of pipe frictional losses in the new arrangement to that in the original configuration would be
-
View Hint View Answer Discuss in Forum
For original configuration
l1 = l
d1 = d
Q1 = Q
For new configuration
l2 = 21
d2 = 2d
Q2 = 2Q
Head loss due to friction,hf = flV² 2gb
where f = friction factor
l = Length of pipe
v = Average velocity
d = Diameter pipeDischarge: Q = AV = π a²V 4 or V = 4Q πa² hf = fl × 
4Q 
² = 8flQ² 2gd πa² πga5
For new Pipe,hf2 = 8fl1Q2² = 8f × 2f × 4Q² = 2fQ² πgda5 π × 25 × a5 πga5 h1 = 2flQ² × πga5 = 1 h2² πga5 2flQ² 4 Correct Option: A
For original configuration
l1 = l
d1 = d
Q1 = Q
For new configuration
l2 = 21
d2 = 2d
Q2 = 2Q
Head loss due to friction,hf = flV² 2gb
where f = friction factor
l = Length of pipe
v = Average velocity
d = Diameter pipeDischarge: Q = AV = π a²V 4 or V = 4Q πa² hf = fl × 
4Q 
² = 8flQ² 2gd πa² πga5
For new Pipe,hf2 = 8fl1Q2² = 8f × 2f × 4Q² = 2fQ² πgda5 π × 25 × a5 πga5 h1 = 2flQ² × πga5 = 1 h2² πga5 2flQ² 4

