Fluid Mechanics and Hydraulic Machinery Miscellaneous
- A water container is kept on a weighing balance. Water from a tap is falling vertically into the container with a volume flow rate of Q; the velocity of the water when it hits the water surface is U. At a particular instant of time the total mass of the container and water is m. The force registered by the weighing balance at this instant of time is
-
View Hint View Answer Discuss in Forum
Volume flow rate = Q
Mass of water strike = ρQ
Velocity of the water when it hit the water surface = U
Force on weighing balance due to water strike = Initial momentum – final momentum
= ρQU – 0= ρQU
(since final velocity is perpendicular to initial velocity)
Now total force on weighing balance = mg + ρQUCorrect Option: A
Volume flow rate = Q
Mass of water strike = ρQ
Velocity of the water when it hit the water surface = U
Force on weighing balance due to water strike = Initial momentum – final momentum
= ρQU – 0= ρQU
(since final velocity is perpendicular to initial velocity)
Now total force on weighing balance = mg + ρQU
- A fan in the duct shown below sucks air from the ambient and expels it as a jet at 1 m/s to the ambient. Determine the gauge pressure at the point marked as A. Take the density of air as 1 kg/m3.
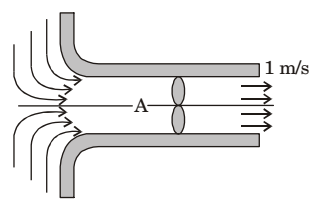
-
View Hint View Answer Discuss in Forum
Applying Bernoulli’s equation between sections (i) & A
P1 = PA + VA² ρg 2g PA - P1 = -VA² ρg 2g
P1 = Pambient
∴ PA - P1 = (PA)gauge∴ (PA)gauge == -VA² ρg 2g (PA)gauge = -1 × 1² = 0.5N/m² 2
Correct Option: A
Applying Bernoulli’s equation between sections (i) & A
P1 = PA + VA² ρg 2g PA - P1 = -VA² ρg 2g
P1 = Pambient
∴ PA - P1 = (PA)gauge∴ (PA)gauge == -VA² ρg 2g (PA)gauge = -1 × 1² = 0.5N/m² 2
- A two-dimensional incompressible frictionless flow field is given by μ = xi - yj. If ρ is the density of the fluid, the expression for pressure gradient vector at any point in the flow field is given as
-
View Hint View Answer Discuss in Forum
NA
Correct Option: D
NA
- For a steady flow, the velocity field is V = (–x² + 3y) i + (2xy)j. The magnitude of the acceleration of a particle at (1, - 1) is
-
View Hint View Answer Discuss in Forum
NA
Correct Option: C
NA
- For a two-dimensional flow, the velocity field is
u = x i + y j x² + y² x² + y²
where i and j are the basis vectors in the x – y Cartesian coordinate system. Identify the CORRECT statements from below.
1. The flow is incompressible
2. The flow is unsteady
3. y-component of acceleration,ay = - y (x² + y²)²
4. x-component of acceleration,ax = -(x + y) (x² + y²)²
-
View Hint View Answer Discuss in Forum
axu δu + v δu δx δy 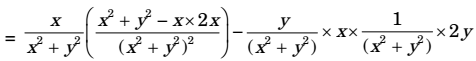
= x(x² + y² -2x²)-2xy² = - x3 - xy² (x² + y²)(x² + y²) (x² + y²) ∴ ax = x (x² + y²)² ay = u δv + v δv δx δy 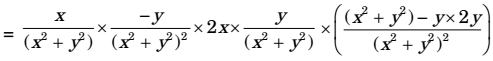
= -x² + yx² - y3 = - y (x² + y²)3 (x² + y²)²
The velocity components are not functions of time, so flow is steady according to continuity equation,
Since it satisfies the above continuity equation for 2D and incompressible flow.
∴ The flow is incompressible.Correct Option: B
axu δu + v δu δx δy 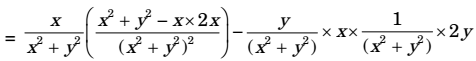
= x(x² + y² -2x²)-2xy² = - x3 - xy² (x² + y²)(x² + y²) (x² + y²) ∴ ax = x (x² + y²)² ay = u δv + v δv δx δy 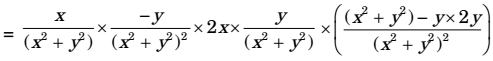
= -x² + yx² - y3 = - y (x² + y²)3 (x² + y²)²
The velocity components are not functions of time, so flow is steady according to continuity equation,
Since it satisfies the above continuity equation for 2D and incompressible flow.
∴ The flow is incompressible.

