Fluid Mechanics and Hydraulic Machinery Miscellaneous
- An aluminium alloy (density 2600 kg/m3) casting is to be produced. A cylindrical hole of 100 mm diameter and 100 mm length is made in the casting using sand core (density 1600 kg/m3). The net buoyancy force (in Newton) acting on the core is _______.
-
View Hint View Answer Discuss in Forum
d = 1600 kg/m3
ρ = 2600 kg/m3
Net buouancy force = weight of liquid displaced – weight of solid body
= v × ρ × g – v × d × g = vg (ρ – d)= π = d² L × g (ρ - d) 4 = π × 0.1² × 0.1 × 9.81 (2600 - 1600) 7.7 N. 4
Correct Option: A
d = 1600 kg/m3
ρ = 2600 kg/m3
Net buouancy force = weight of liquid displaced – weight of solid body
= v × ρ × g – v × d × g = vg (ρ – d)= π = d² L × g (ρ - d) 4 = π × 0.1² × 0.1 × 9.81 (2600 - 1600) 7.7 N. 4
- For a completely submerged body with centre of gravity G and centre of buoyancy B, the condition of stability will be
-
View Hint View Answer Discuss in Forum
A body in a liquid is said to be stable, when given small displacement, it returns to its original position.
Stability of completely submerged Bodies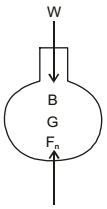
The center of gravity ‘G’ is below the center of Buoyancy ‘B’.Correct Option: A
A body in a liquid is said to be stable, when given small displacement, it returns to its original position.
Stability of completely submerged Bodies
The center of gravity ‘G’ is below the center of Buoyancy ‘B’.
- Two immiscible, incompressible, viscous fluids having same densities but different viscosities are contained between two infinite horizontal parallel plates. 2 m apart as shown below. The bottom plate is fixed and the upper plate move to the right with a constant velocity of 3 m/s. With the assumptions of Newtonian fluid steady, and fully developed laminar flow with zero pressure gradient in all directions, the momentum equations simplify to
d²u = 0 dy²
If the dynamic viscosity of the lower fluid, μ2 is twice that of the input fluid, μ1, then the velocity at the interface (round off to two decimal places) is_____m/s.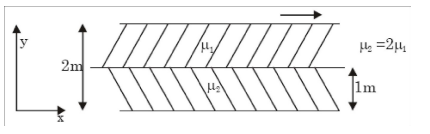
-
View Hint View Answer Discuss in Forum

μ² = 2μ1
V2 = 3 m/s
Shear stress value at intermediate plate will beτ = μ2V1 = μ1(V2 - V1) h h
Since μ2 = 2μ1
∴ 2V1 = V1 – V1
⇒ V2 = V1 +2V1
V2 = 3V1 [V2 = 3 m/s]
&rARr; 3 = 3V1⇒V1 = 3 = 1 m/s 3
Correct Option: A

μ² = 2μ1
V2 = 3 m/s
Shear stress value at intermediate plate will beτ = μ2V1 = μ1(V2 - V1) h h
Since μ2 = 2μ1
∴ 2V1 = V1 – V1
⇒ V2 = V1 +2V1
V2 = 3V1 [V2 = 3 m/s]
&rARr; 3 = 3V1⇒V1 = 3 = 1 m/s 3
- The SI unit of kinematic viscosity v is
-
View Hint View Answer Discuss in Forum
Kinematic Viscosity:
v = Dynamic viscosity = μ Density ρ v = μ = Ns / m² ρ kg / m3 = kg.m × s × 1 s² m² kg / m3
= m²/sCorrect Option: A
Kinematic Viscosity:
v = Dynamic viscosity = μ Density ρ v = μ = Ns / m² ρ kg / m3 = kg.m × s × 1 s² m² kg / m3
= m²/s
- Match List-I with List-II and select the correct answer using the codes given below the lists:
List-I
P. Centrifugal compressor
Q. Centrifugal pump
R. Pelton wheel
S. Kaplan turbine
List-II
1. Axial flow
2. Surging
3. Priming
4. Pure impulse enter codes:
-
View Hint View Answer Discuss in Forum
Kaplan – Axial flow Pelton – Impulse type
Correct Option: A
Kaplan – Axial flow Pelton – Impulse type

