Fluid Mechanics and Hydraulic Machinery Miscellaneous
Direction: Consider a steady incompressible flow through a channel as shown below:
The velocity profile is uniform with a value of u0 at the inlet section A. The velocity profile at section B downstream is
- The ratio Vm/u0 is
-
View Hint View Answer Discuss in Forum
Applying continuity equation at sections A and B, mass flow rate at inlet section A = mass rate at section B.
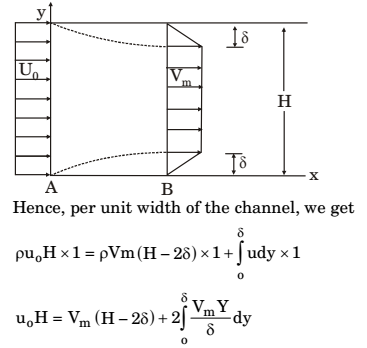

∴ u = VmY 
δ u0H = Vm(H − 2δ) + 2 Vm 
Y² 
δ δ 2 0 u0H = Vm(H − 2δ) + 2 Vm × δ² δ 2
u0H = Vm(H − 2δ) + Vmδ
u0H = VmH − 2Vmδ + Vmδ
u0H = VmH − Vmδ
u0H = Vm(H − δ)or Vm = H = 1 u0 H − δ 1 − (δ/H) Correct Option: C
Applying continuity equation at sections A and B, mass flow rate at inlet section A = mass rate at section B.


∴ u = VmY 
δ u0H = Vm(H − 2δ) + 2 Vm 
Y² 
δ δ 2 0 u0H = Vm(H − 2δ) + 2 Vm × δ² δ 2
u0H = Vm(H − 2δ) + Vmδ
u0H = VmH − 2Vmδ + Vmδ
u0H = VmH − Vmδ
u0H = Vm(H − δ)or Vm = H = 1 u0 H − δ 1 − (δ/H)
- In a Pelton wheel, the bucket peripheral speed is 10 m/s, the water jet velocity is 25 m/s and volumetric flow rate of the jet is 0.1 m3/s. If the jet deflection angle is 120° and the flow is ideal, the power developed is
-
View Hint View Answer Discuss in Forum
u = 10 m/s
Vi = 25 m/s
Q = 0.1 m3 /s
Jet deflection angle = 120°
∴ β = 180° – 120° = 60°
P = ρQ (Vi – u)(1 + cosβ)u
P = 1000 × 0.1(25 – 10)(1 + cos60°) × 10 P = 22500 W = 22.5 kWCorrect Option: C
u = 10 m/s
Vi = 25 m/s
Q = 0.1 m3 /s
Jet deflection angle = 120°
∴ β = 180° – 120° = 60°
P = ρQ (Vi – u)(1 + cosβ)u
P = 1000 × 0.1(25 – 10)(1 + cos60°) × 10 P = 22500 W = 22.5 kW
- Water flows through a 10 mm diameter and 250 m long smooth pipe at an average velocity of 0.1 m/s. The density and the viscosity of water are 997 kg/m3 and 855 × 10–6 Ns/m2, respectively. Assuming fully- developed flow, the pressure drop (in Pa) in the pipe is ____?
-
View Hint View Answer Discuss in Forum
Re = ρVD μ Re = 997 × 0.1 × 10 × 10-3 = 1166.081 ( laminar flow ) 855 × 10-6 f = 64 = 64 = 0.054 Re 1166.081 ∆p = f l ρV2 2D = 0.054 × 250 × 997 × (0.1)2 = 6840 pascal 2 × 10 × 10-3
Correct Option: A
Re = ρVD μ Re = 997 × 0.1 × 10 × 10-3 = 1166.081 ( laminar flow ) 855 × 10-6 f = 64 = 64 = 0.054 Re 1166.081 ∆p = f l ρV2 2D = 0.054 × 250 × 997 × (0.1)2 = 6840 pascal 2 × 10 × 10-3
- A fluid of dynamic viscosity 2 × 10–5 kg/ms and density 1 kg/m3 flows with an average velocity of 1 m/s through a long duct of rectangular (25 mm × 15 mm) cross-section, Assuming laminar flow, the pressure drop (in Pa) in the fully developed region per meter length of the duct is _______.
-
View Hint View Answer Discuss in Forum
Given, μ = 2 × 10– 5 kg/m.s, ρ = 1 kg/m³, uav = 1m/sec
Duct area = 25 mm × 15 mm∴ ∆P = 4 × λ × ρ × U²av ..........(i) L 2 × Dn
Here λ = Friction factor
Dn = Dia∴ Dn = 4 × A (A = Area, P = Parameter) P λ = 4 × 25 × 15 = 18.75 mm .......(ii) 2(25 + 15) λ = 16 ∴ Re = ρ.uav.Dn Re π ∴ Re = 1 × 1 × 18.75 × 10-3 = 937.5 2 × 10-5 ∴ λ = 16 = 1.707 × 10-2..........(iii) 937.5
Here from equation (3),∆P = 4 × 1.707 × 10-2 × (1)² × 2 = 1.82.8 Pa/m. L 2 × 18.75 × 10-3
V1 = √2gHCorrect Option: B
Given, μ = 2 × 10– 5 kg/m.s, ρ = 1 kg/m³, uav = 1m/sec
Duct area = 25 mm × 15 mm∴ ∆P = 4 × λ × ρ × U²av ..........(i) L 2 × Dn
Here λ = Friction factor
Dn = Dia∴ Dn = 4 × A (A = Area, P = Parameter) P λ = 4 × 25 × 15 = 18.75 mm .......(ii) 2(25 + 15) λ = 16 ∴ Re = ρ.uav.Dn Re π ∴ Re = 1 × 1 × 18.75 × 10-3 = 937.5 2 × 10-5 ∴ λ = 16 = 1.707 × 10-2..........(iii) 937.5
Here from equation (3),∆P = 4 × 1.707 × 10-2 × (1)² × 2 = 1.82.8 Pa/m. L 2 × 18.75 × 10-3
V1 = √2gH
- Cavitation in a hydraulic reaction turbine is most likely to occur at the turbine
-
View Hint View Answer Discuss in Forum
NA
Correct Option: D
NA

