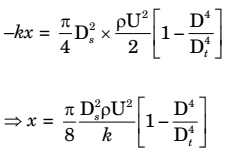-
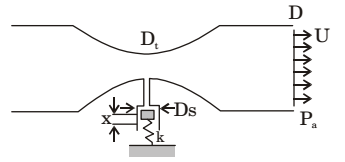
Air flows through a venturi and into atmosphere. Air density is ρa; atmospheric pressure is ρa; throat diameter is Dt; exit diameter is D and exit velocity is U. The throat is connected to a cylinder containing a friction less piston attached to a spring. The spring constant is k. The bottom surface of the piston is exposed to atmosphere. Due to the flow, the piston moves by distance x. Assuming in compressible friction less flow, x is
-
- (ρU2/2k)πD2s
-
(ρU2/8k) 
D2 - 1 
πD2s D2t -
(ρU2/2k) 
D2 - 1 
πD2s D2t -
(ρU2/8k) 
D4 - 1 
πD2s D4t
Correct Option: D
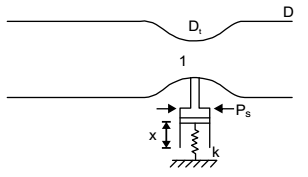
Applying Bernoulli’s equation at points (1) and (2), we have
| + | + z1 = | + | + z2 | |||||
| ρg | 2g | ρg | 2g |
Since venturi is horizontal
z1 = z2
| Now | - | = | - | |||||
| ρg | ρg | 2g | 2g |
| ⇒(p1 - p2) = | (v22 - v21) = | = (v22 - v21) | ||
| 2g | g |
Since P2 = Pa = atmospheric pressure
| ∴ (P2 - Pa) | (v22 - v21) ........(i) | 2 |
Applying continuity equation at points (i) and (ii), we have
A1 v1 = A2 v2
| ⇒ v1 = |  |  | v2 since V2 = U | A1 |

| v1 = |  |  | 2 | U | Dt |
From equation (i),
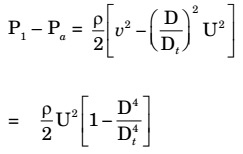
At point P
Spring force = pressure force due air