-
Air flows at the rate of 1.5 m3/s through a horizontal pipe with a gradually reducing crosssection as shown in the figure. The two crosssections of the pipe have diameters of 400 mm and 200 mm. Take the air density as 1.2 kg/m3 and assume inviscid incompressible flow. The change in pressure (p2 – p1) (in kPa) between sections 1 and 2 is
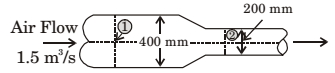
-
- –1.28
- 2.56
- –2.13
- 1.28
Correct Option: A
| + | + Z1 = | + | + Z2 [Z = constant] | ||||
| δg | 2g | δg | 2g |
| A1 = | × 0.4² = 0.1256 m² | |
| 2 |
| A2 = | × 0.2² = 0.314 m² | |
| 4 |
| = | ||
| δg | 2g |
| = |  | − |  | ||||
| 1.2 | 2 | A1² | A2² |
| P2 − P1 = 0.6 × (1.5)² |  | − |  | ||
| A1² | A2² |
| P2 − P1 = 1.35 |  | − |  | ||
| 0.01577 | 0.00985 |
= 1.35 [63.41 – 1015.22]
= –1.28 ×10³ Pascal
= – 1.28 kPa

