The radial component of the fluid acceleration at r = R

Home » Fluid Mechanics and Hydraulic Machinery » Fluid Mechanics and Hydraulic Machinery Miscellaneous » Question

Direction: The gap between a moving circular plate and a stationary surface is being continuously reduced, as the circular plate comes down at a uniform speed V towards the stationary bottom surface, as shown in the figure. In the process, the fluid contained between the two plates flows out radially. The fluid is assumed to be incompressible and inviscid.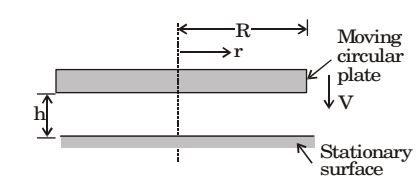

The radial component of the fluid acceleration at r = R is

1. 3V²R
  4h²
2. V²R
  4h²
3. V²R
  2h²
4. V²h
  2R²

Correct Option: A

Radial acceleration

a_r = V_r ×	∂V_r	+	∂V_r
	∂r		∂t

a_r =	V.r	×	∂		V.r		+	∂		V.r
	2h		∂r		2h			∂t		2h

-∂h	= V
∂t

∴ a_r =	V.r	×	V.r	+	V.r	×		-1	∂h
	2h		2h		2			h²	∂t

∴ a_r =	V²r	+	2V²r
	4h²		4h²

a_r =	3V²r
	4h²

	3V²R
	4h²

	V²R
	4h²

	V²R
	2h²

	V²h
	2R²