A leaf is caught in a whirlpool. At a given instant, the

A leaf is caught in a whirlpool. At a given instant, the leaf is at a distance of 120 m from the centre of the whirlpool. The whirlpool can be described by the following velocity distribution:
V_r = - 60 × 10³ m/s and V_θ = 300 × 10³ m/s
2πr 2πr

where r (in meters) is the distance from the centre of the whirlpool. What will be the distance of the leaf from the centre when it has moved through half a revolution?

Radial distance = 120 m

V_r = -	60 × 10³	m /s
	2πr

& V_θ =	300 × 10³	m /s
	2πr

& θ = π

	V_r	=	-1
	V_θ		5

we know that

V_r =	dr	...(i)
	dt

& V_θ = rw = r	dθ
	dt

-5V_r = r	dθ
	dt

V_r =	-r	×	dθ	...(ii)
	5		dt

By equating (i) & (ii), we get

dr	=	-r	.	dθ
dt		5		dt

Integrating both sides, we get

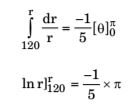
ln		r		=	-π
		120			5

By solving above, we get
r = 64 m