Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. The smallest finite automata which accepts the language {x| length of x is divisible by 3} has








  1. View Hint View Answer Discuss in Forum

    Answer in the book is wrong

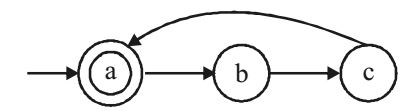
    Start & end are same as (a) hence the minimum no. of states required are3. Option (b) is correct. If string traversal doesn't stop at (a) then string length is not divisibleby 3.

    Correct Option: B

    Answer in the book is wrong

    Start & end are same as (a) hence the minimum no. of states required are3. Option (b) is correct. If string traversal doesn't stop at (a) then string length is not divisibleby 3.

  1. The finite state machine described by the following state diagram with A as starting state, where
    an arc label is
    x
    		 and x stands for 1-bit input and y stands for 2 bit output
    y









  1. View Hint View Answer Discuss in Forum

    As per the given diagram.

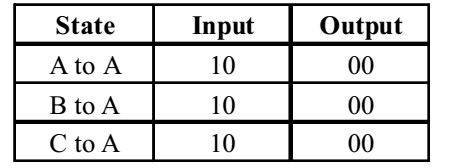
    Therefore, the finite state machine outputs the sum of the present and previous bits of the input.

    Correct Option: A

    As per the given diagram.

    Therefore, the finite state machine outputs the sum of the present and previous bits of the input.

  1. Consider the NFA, M, shown below:

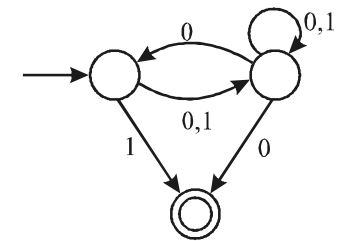
    Let the language accepted by M be L. Let L1 be the language accepted by the NFA M1 obtained by changing the accepting state of M to a non-accepting state and by changing the non-accepting state of M to accepting states. Which of the following statements is true?








  1. View Hint View Answer Discuss in Forum

    The given machine M is

    Now, the complementary machine M is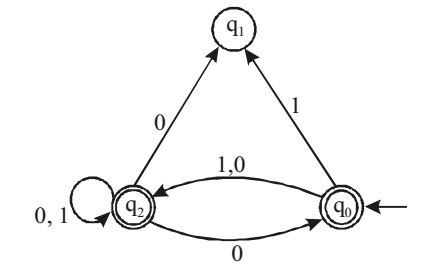

    In the case of DFA, L(M) = L(M) but in the case of nfa this is not true. Infact L(M) and L (M) have no connection.
    To find L1 = L(M), we have to look at M and directly find its language.
    Clearly, λ = L(M), since q0 is accepting it (0 + 1) (0 + 1)* ∈ L(M), since q2 is accepting it.
    ∴ L(M) = L1 = l + (0 + 1) (0 + 1)*
    ∴ L1 = (0 + 1)* = {0, 1}*

    Correct Option: B

    The given machine M is

    Now, the complementary machine M is

    In the case of DFA, L(M) = L(M) but in the case of nfa this is not true. Infact L(M) and L (M) have no connection.
    To find L1 = L(M), we have to look at M and directly find its language.
    Clearly, λ = L(M), since q0 is accepting it (0 + 1) (0 + 1)* ∈ L(M), since q2 is accepting it.
    ∴ L(M) = L1 = l + (0 + 1) (0 + 1)*
    ∴ L1 = (0 + 1)* = {0, 1}*

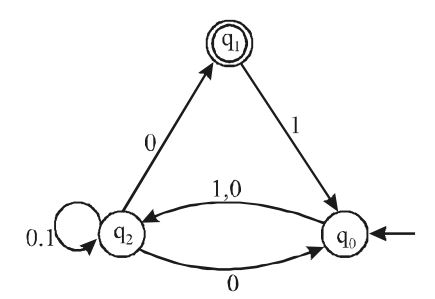
  1. Consider the finite automata in the following figure.

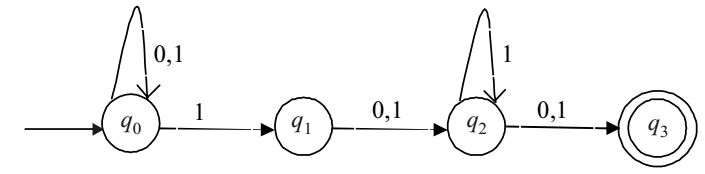
    Which is the set of reachable states for the input string 0011?








  1. View Hint View Answer Discuss in Forum

    Following paths can be taken by the finite Automata for the input string “0011”:––


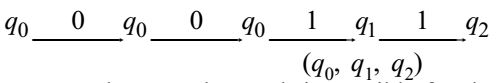
    We note that no other path is possible for the input string "0011". So, finally union of all three cases gives us the set of Reachable states which is {q0, q1, q2}

    Correct Option: A

    Following paths can be taken by the finite Automata for the input string “0011”:––


    We note that no other path is possible for the input string "0011". So, finally union of all three cases gives us the set of Reachable states which is {q0, q1, q2}

  1. Which of the regular expressions given below represent the following DFA?

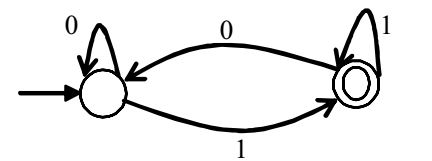
    I 0*1(1+00*1)*
    II 0*1*1+11*0*1
    III (0+1)*1








  1. View Hint View Answer Discuss in Forum

    (I) 0 *1(1 + 0 0 *1)*
    (II) 0 *1*1+11*0 *1
    (III) (0 +1)*1
    (I) and (III) represent DFA.
    (II) Doesn't represent as the DFA accepts strings like 11011, but the given regular expression doesn't accept.

    Correct Option: B

    (I) 0 *1(1 + 0 0 *1)*
    (II) 0 *1*1+11*0 *1
    (III) (0 +1)*1
    (I) and (III) represent DFA.
    (II) Doesn't represent as the DFA accepts strings like 11011, but the given regular expression doesn't accept.