Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. Which of the following is true?









  1. View Hint View Answer Discuss in Forum

    Finite subset of non-regular set is regular as we know that Pumping Lemma can be applied on all the finite sets that states that all finite sets are regular. Infinite union of finite set is not regular because regular sets can never be closed under infinite union.

    Correct Option: B

    Finite subset of non-regular set is regular as we know that Pumping Lemma can be applied on all the finite sets that states that all finite sets are regular. Infinite union of finite set is not regular because regular sets can never be closed under infinite union.

  1. Given below are two finite state automata ( → indicates the start state and F indicates a final state)

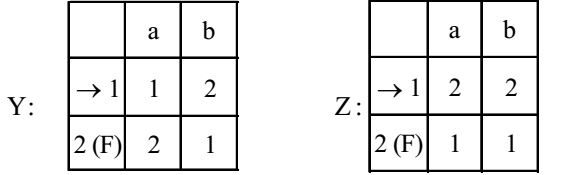
    Which of the following represents the product automata Z × Y?








  1. View Hint View Answer Discuss in Forum

    Given : Transition table for Y and Z
    The number of states of Z = 2
    The number of states of Y = 2
    Z × Y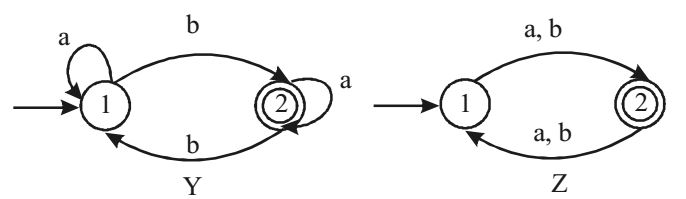

    No. of states of the product of Z and Y = 2 × 2 = 4
    Now, the states as per the given options are P, Q, R and S. The finite state automata is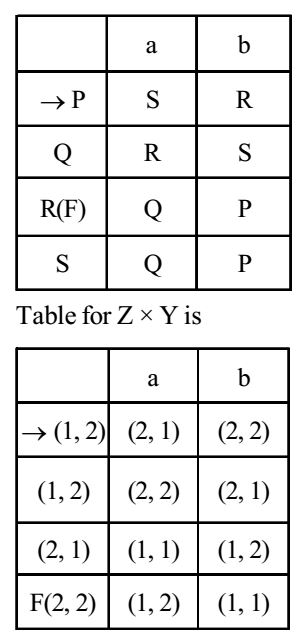

    Correct Option: A

    Given : Transition table for Y and Z
    The number of states of Z = 2
    The number of states of Y = 2
    Z × Y

    No. of states of the product of Z and Y = 2 × 2 = 4
    Now, the states as per the given options are P, Q, R and S. The finite state automata is

  1. Let L = {W ∈ (0, 1) * | W has even number of 1s}, i.e., L is the set of all bit strings with even number of 1's. Which one of the regular expressions below represents L?








  1. View Hint View Answer Discuss in Forum

    It is given that L is the set of all bit strings with even number of 1's so the regular expression should exhibit the same. Now, the min string should be e and the string should be e, 0, 11, 101,... The string obtained from such expression is 0* (10* 10 *)*

    Correct Option: B

    It is given that L is the set of all bit strings with even number of 1's so the regular expression should exhibit the same. Now, the min string should be e and the string should be e, 0, 11, 101,... The string obtained from such expression is 0* (10* 10 *)*

  1. S → aSa |bSb| a | b; The language generated by the above grammar over the alphabet {a, b} is the set of








  1. View Hint View Answer Discuss in Forum

    Given grammar S → aSabSbab. The strings generated through this grammar is definitely palindromes,but not all it can only generate palindromes of odd length only so (A) & (D) are false, (B) is correct. Also it can generate palindromes which start and end with same symbol, but not all strings eg. aabababba .

    Correct Option: B

    Given grammar S → aSabSbab. The strings generated through this grammar is definitely palindromes,but not all it can only generate palindromes of odd length only so (A) & (D) are false, (B) is correct. Also it can generate palindromes which start and end with same symbol, but not all strings eg. aabababba .


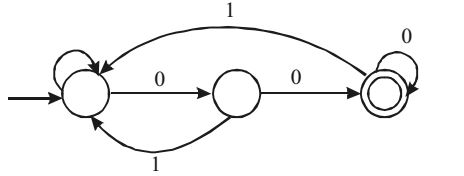
  1. The above DFA accepts the set of all strings over {0, 1} that








  1. View Hint View Answer Discuss in Forum


    Therefore, the above DFA ends with 00.

    Correct Option: C


    Therefore, the above DFA ends with 00.