Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. Consider the NFA, M, shown below:

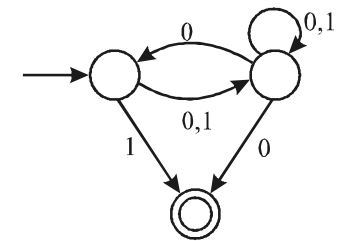
    Let the language accepted by M be L. Let L1 be the language accepted by the NFA M1 obtained by changing the accepting state of M to a non-accepting state and by changing the non-accepting state of M to accepting states. Which of the following statements is true?








  1. View Hint View Answer Discuss in Forum

    The given machine M is

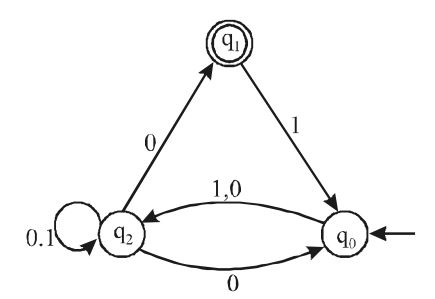
    Now, the complementary machine M is

    In the case of DFA, L(M) = L(M) but in the case of nfa this is not true. Infact L(M) and L (M) have no connection.
    To find L1 = L(M), we have to look at M and directly find its language.
    Clearly, λ = L(M), since q0 is accepting it (0 + 1) (0 + 1)* ∈ L(M), since q2 is accepting it.
    ∴ L(M) = L1 = l + (0 + 1) (0 + 1)*
    ∴ L1 = (0 + 1)* = {0, 1}*

    Correct Option: B

    The given machine M is

    Now, the complementary machine M is

    In the case of DFA, L(M) = L(M) but in the case of nfa this is not true. Infact L(M) and L (M) have no connection.
    To find L1 = L(M), we have to look at M and directly find its language.
    Clearly, λ = L(M), since q0 is accepting it (0 + 1) (0 + 1)* ∈ L(M), since q2 is accepting it.
    ∴ L(M) = L1 = l + (0 + 1) (0 + 1)*
    ∴ L1 = (0 + 1)* = {0, 1}*

  1. The finite state machine described by the following state diagram with A as starting state, where
    an arc label is
    x
    		 and x stands for 1-bit input and y stands for 2 bit output
    y









  1. View Hint View Answer Discuss in Forum

    As per the given diagram.

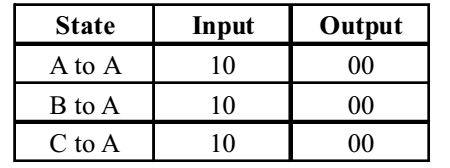
    Therefore, the finite state machine outputs the sum of the present and previous bits of the input.

    Correct Option: A

    As per the given diagram.

    Therefore, the finite state machine outputs the sum of the present and previous bits of the input.

  1. The smallest finite automata which accepts the language {x| length of x is divisible by 3} has








  1. View Hint View Answer Discuss in Forum

    Answer in the book is wrong

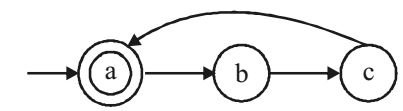
    Start & end are same as (a) hence the minimum no. of states required are3. Option (b) is correct. If string traversal doesn't stop at (a) then string length is not divisibleby 3.

    Correct Option: B

    Answer in the book is wrong

    Start & end are same as (a) hence the minimum no. of states required are3. Option (b) is correct. If string traversal doesn't stop at (a) then string length is not divisibleby 3.

  1. Let S and T be languages over ∑ = {a, b} represented by the regular expressions (a + b*)* and (a + b)*, respectively. Which of the following is true?








  1. View Hint View Answer Discuss in Forum

    Lets consider the regular expressions as given in the questions:

    Second, (a + b)*

    ⇒ (a + b*)* = (a + b*) Therefore, we can say that S = T

    Correct Option: C

    Lets consider the regular expressions as given in the questions:

    Second, (a + b)*

    ⇒ (a + b*)* = (a + b*) Therefore, we can say that S = T

  1. Consider the following context-free grammar over the alphabet ∑ = {a, b, c} with S as the start symbol:
    S → abScT | abcT
    T → bT | b
    Which one of the following represents the language generated by the above grammar?








  1. View Hint View Answer Discuss in Forum

    The given context free Grammar
    ∑ = {a , b , c} with S as the start symbol.
    S → abScT/ abcT
    T → bT/ b
    The minimum length string generated by the grammar is 1.
    Consider first case ( S → abcT ) then ( S → abcb ) .
    Hence all the variable s are greater than 1.
    Consider second case
    S → abScT
    → ababScTcT
    → ababScTcTcT .............................. ..............................
    → (ab)n (CT)n
    Here T can generate any number of b's string with single b, so (T = bm)
    Hence, the language is
    L = [ (ab)n ( cbm )n | m , n ≥ 1 ]
    Hence option (c) is correct.

    Correct Option: C

    The given context free Grammar
    ∑ = {a , b , c} with S as the start symbol.
    S → abScT/ abcT
    T → bT/ b
    The minimum length string generated by the grammar is 1.
    Consider first case ( S → abcT ) then ( S → abcb ) .
    Hence all the variable s are greater than 1.
    Consider second case
    S → abScT
    → ababScTcT
    → ababScTcTcT .............................. ..............................
    → (ab)n (CT)n
    Here T can generate any number of b's string with single b, so (T = bm)
    Hence, the language is
    L = [ (ab)n ( cbm )n | m , n ≥ 1 ]
    Hence option (c) is correct.