E → E - T |
T → T + F | F
F → ( E ) | id
Using the rule for removal of left recursion is
A → Aα / β
A → βA '
A ' → α A ' / ∈
Then, the given grammar is written as :-
E' → −TE' / ∈
E → +TE '
T ' → + FT ' / ∈
T → FT '
F → (E) | id
Now by putting E ' as X and T ' as Y, then
X → −TX / ∈
E → TX
Y → +FY / ∈
T → FY
F → (E) | id
Hence option (c) is correct.

Correct Option: C

E → E - T |
T → T + F | F
F → ( E ) | id
Using the rule for removal of left recursion is
A → Aα / β
A → βA '
A ' → α A ' / ∈
Then, the given grammar is written as :-
E' → −TE' / ∈
E → +TE '
T ' → + FT ' / ∈
T → FT '
F → (E) | id
Now by putting E ' as X and T ' as Y, then
X → −TX / ∈
E → TX
Y → +FY / ∈
T → FY
F → (E) | id
Hence option (c) is correct.

The number of control Paths is depends on number of if statement that is 2ⁿ, where, n is the number. of if statements For (2 “if statements”) 2² = 4 control flow Paths are possible :

These four control flow are :
(1) e₁ → e₂
(2) e₁ → e₃
(3) (e₂ if e₄ ) → e₅
(4) (e₃ if e₄ ) → e₅
So, for (10 “if statements”), 2¹⁰ = 1024.
Control flow path are possible. Hence, answer is 1024.

Correct Option: A

The number of control Paths is depends on number of if statement that is 2ⁿ, where, n is the number. of if statements For (2 “if statements”) 2² = 4 control flow Paths are possible :

These four control flow are :
(1) e₁ → e₂
(2) e₁ → e₃
(3) (e₂ if e₄ ) → e₅
(4) (e₃ if e₄ ) → e₅
So, for (10 “if statements”), 2¹⁰ = 1024.
Control flow path are possible. Hence, answer is 1024.

The context free grammar given over alphabets
∑ = {a, b, c}, with S and T are nonterminals.
Given, G₁ : S → aSb | T , T → cT | ∈
G₂ : S → bSa | T , T → cT | ∈
Lets L(G₁) is the language for Grammar (G₁) and L(G₂) is the language for Grammar (G₂).
where L(G₁) = { aⁿ c^m bⁿ | m , n ≥ 0 }
L(G₂) = { bⁿ c^m aⁿ | m , n ≥ 0 }
then L(G₁) ∩ L(G₂) = { aⁿ c^m bⁿ } ∩ { bⁿ c^m aⁿ }
= { c^m | m ≥ 0 } = C^*
Since the only common strings will be those strings with only ‘C’, so the intersection is not finite but regular.

Correct Option: B

The context free grammar given over alphabets
∑ = {a, b, c}, with S and T are nonterminals.
Given, G₁ : S → aSb | T , T → cT | ∈
G₂ : S → bSa | T , T → cT | ∈
Lets L(G₁) is the language for Grammar (G₁) and L(G₂) is the language for Grammar (G₂).
where L(G₁) = { aⁿ c^m bⁿ | m , n ≥ 0 }
L(G₂) = { bⁿ c^m aⁿ | m , n ≥ 0 }
then L(G₁) ∩ L(G₂) = { aⁿ c^m bⁿ } ∩ { bⁿ c^m aⁿ }
= { c^m | m ≥ 0 } = C^*
Since the only common strings will be those strings with only ‘C’, so the intersection is not finite but regular.

The given grammar with productions,
S → SaS | aSb | bSa | SS | ∈
Now consider,
S → aSb | bSa | SS | ∈
This grammar generates all strings with equal number of ‘a’ and ‘b’.
Now, S → SaS can only generate strings where ‘a’ is more than ‘b’. Since on left and right of ‘a’ in SaS, S will have only strings with n_a = n_b or n_a > n_b.
Now consider each options
1. S → SS → aSbS → abS → abaSb → abab ,when, S → ∈
2. S → aSb → aSaSb → aaaSb → aaab , when S → ∈
3. S → SS → aSbS → abS → abbSa → abbSaSa → abbaa, when ( S → ∈ )
4. “babba” which is a string with nb > na is not possible to generate by the given grammar.
Hence, option (d) is correct.

Correct Option: D

The given grammar with productions,
S → SaS | aSb | bSa | SS | ∈
Now consider,
S → aSb | bSa | SS | ∈
This grammar generates all strings with equal number of ‘a’ and ‘b’.
Now, S → SaS can only generate strings where ‘a’ is more than ‘b’. Since on left and right of ‘a’ in SaS, S will have only strings with n_a = n_b or n_a > n_b.
Now consider each options
1. S → SS → aSbS → abS → abaSb → abab ,when, S → ∈
2. S → aSb → aSaSb → aaaSb → aaab , when S → ∈
3. S → SS → aSbS → abS → abbSa → abbSaSa → abbaa, when ( S → ∈ )
4. “babba” which is a string with nb > na is not possible to generate by the given grammar.
Hence, option (d) is correct.

As per the given diagram.

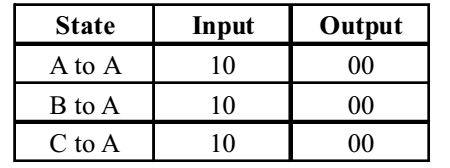
Therefore, the finite state machine outputs the sum of the present and previous bits of the input.

Correct Option: A

As per the given diagram.

Therefore, the finite state machine outputs the sum of the present and previous bits of the input.