Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. Which of the following statements is false?








  1. View Hint View Answer Discuss in Forum

    Option (a) True : Non-deterministic finite automata can be converted into the deterministic finite automata.
    Option (b) True : With reference to option (a), same is with the non-deterministic turing machine.
    Option (c) True : Regular language is always contextfree but the reverse is not true.
    Option (d) False : We know that a set is a subset of itself and hence, every subset of recursively enumerable set is not recursive.

    Correct Option: D

    Option (a) True : Non-deterministic finite automata can be converted into the deterministic finite automata.
    Option (b) True : With reference to option (a), same is with the non-deterministic turing machine.
    Option (c) True : Regular language is always contextfree but the reverse is not true.
    Option (d) False : We know that a set is a subset of itself and hence, every subset of recursively enumerable set is not recursive.

  1. Which of the following are regular sets?
    1. { an b2m | n ≥ 0, m ≥ 0 }
    2. { an bm | n = 2m }
    3. { an bm | n ≠ m }
    4. { xcy | x, y, ∈ {a,b}* }








  1. View Hint View Answer Discuss in Forum

    Lets gather some knowledge for the regular expressions before going to True or False. The regular sets are defined in such a way that they have to follow some conventions. Conventions on regular expressions
    1. Bold face is not used for regular expressions when the expression is not confusing. So, for example, (r + s) is used instead (r + s).
    2. The operation * has precedence over concatenation, which further has precedence over union (+). Thus, the regular expression (a + b(c*))) is written as a + bc*.
    3. The concatenation of k r's, where r is regular expression, is written as rk . Thus, for example rr = r2 . The language corresponding to rk is Lkr , where Lr is language corresponding to the regular expression r. For a recursive definition of Lkr .
    4. The (r+) is used as a regular expression to represent L+r .
    Based on the concept, only 1 and 4 are found to be regular since in 1, L can be written as a* (bb)* and 4, (a + b) * c(a + b)* can be written for the 4.

    Correct Option: A

    Lets gather some knowledge for the regular expressions before going to True or False. The regular sets are defined in such a way that they have to follow some conventions. Conventions on regular expressions
    1. Bold face is not used for regular expressions when the expression is not confusing. So, for example, (r + s) is used instead (r + s).
    2. The operation * has precedence over concatenation, which further has precedence over union (+). Thus, the regular expression (a + b(c*))) is written as a + bc*.
    3. The concatenation of k r's, where r is regular expression, is written as rk . Thus, for example rr = r2 . The language corresponding to rk is Lkr , where Lr is language corresponding to the regular expression r. For a recursive definition of Lkr .
    4. The (r+) is used as a regular expression to represent L+r .
    Based on the concept, only 1 and 4 are found to be regular since in 1, L can be written as a* (bb)* and 4, (a + b) * c(a + b)* can be written for the 4.

  1. Which one of the following languages over the alphabet {0 1} is described by the regular expression (0 + 1) * 0(0 + 1) *?








  1. View Hint View Answer Discuss in Forum

    We are given with the relation
    (0 + 1) * 0(0 + 1)* 0(0 + 1)*
    Here, the accepting languages are L = {00, 000, 100, 001, 010, 0000, 0001, 1000, 1001, 0100, 1100, 0010, 0011, 0110, 0101, 1010,...}
    The common feature in the accepting languages can be seen that they consist of atleast two 0's.

    Correct Option: C

    We are given with the relation
    (0 + 1) * 0(0 + 1)* 0(0 + 1)*
    Here, the accepting languages are L = {00, 000, 100, 001, 010, 0000, 0001, 1000, 1001, 0100, 1100, 0010, 0011, 0110, 0101, 1010,...}
    The common feature in the accepting languages can be seen that they consist of atleast two 0's.

  1. Given the following state table of an FSM with two states A and B, one input and one output

    If the initial state is A = 0, B = 0, what is the minimum length of an input string, which will take the machine to the state A = 0, B = 1 with output = 1?








  1. View Hint View Answer Discuss in Forum

    The initial state = 00
    Final state required = 01
    Let us construct the transition diagram for the given.

    We get the total number of states to be 3 when getting the desired output. The transition diagram can further be elaborated as below.
    There can be 4 states 00, 01, 10, 11.
    With this, the FSM can be designed as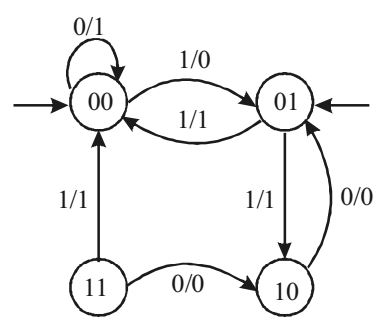

    The desired output is obtained with the input string 101, however, the concern is number of states which we found to be 3.

    Correct Option: A

    The initial state = 00
    Final state required = 01
    Let us construct the transition diagram for the given.

    We get the total number of states to be 3 when getting the desired output. The transition diagram can further be elaborated as below.
    There can be 4 states 00, 01, 10, 11.
    With this, the FSM can be designed as

    The desired output is obtained with the input string 101, however, the concern is number of states which we found to be 3.


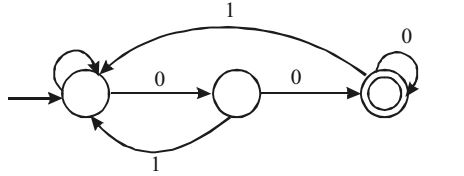
  1. The above DFA accepts the set of all strings over {0, 1} that








  1. View Hint View Answer Discuss in Forum


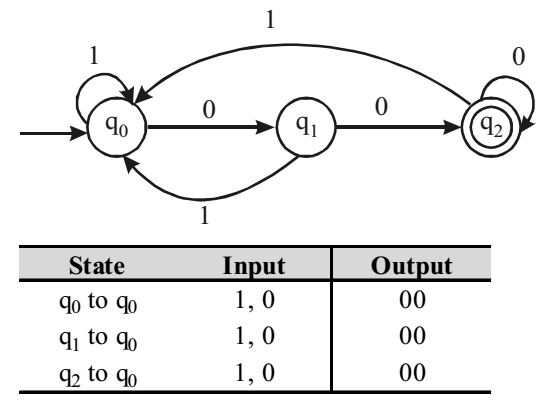
    Therefore, the above DFA ends with 00.

    Correct Option: C


    Therefore, the above DFA ends with 00.