Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. Which one of the following grammars is free from left recursion?








  1. View Hint View Answer Discuss in Forum

    Grammar A has direct left recursion because of the production rule : A → Aa. Grammar C has indirect left recursion because of the production rules : S → Aa and A → Sc Grammar D has indirect left recursion because of production rules : A → Bd and B → Ae Grammar B doesn't have any left recursion (neither direct nor indirect).

    Correct Option: B

    Grammar A has direct left recursion because of the production rule : A → Aa. Grammar C has indirect left recursion because of the production rules : S → Aa and A → Sc Grammar D has indirect left recursion because of production rules : A → Bd and B → Ae Grammar B doesn't have any left recursion (neither direct nor indirect).

  1. Language L1 is defined by the grammar: S1 → aS1 b | ε
    Language L2 is defined by the grammar: S2 → abS2 | ε
    Consider the following statements:
    P : L1 is regular
    Q : L2 is regular
    Which one of the following is TRUE?








  1. View Hint View Answer Discuss in Forum

    L1 has the property that no. of a’s should be equal to no. of b’s in a string, and all a’s should precede all b’s. Hence extra memory will be required to check this property of a string (Finite Automata can't be built for this type of language). Hence this is not regular language. Therefore P is False. L2 has the property that no. of a’s should be equal to no. of b’s, but order of a’s and b’s is different here, it is (ab)*, which will require no extra memory to be accepted. (Finite Automata can be built for this language). Hence L2 is regular language. Therefore Q is True.

    Correct Option: C

    L1 has the property that no. of a’s should be equal to no. of b’s in a string, and all a’s should precede all b’s. Hence extra memory will be required to check this property of a string (Finite Automata can't be built for this type of language). Hence this is not regular language. Therefore P is False. L2 has the property that no. of a’s should be equal to no. of b’s, but order of a’s and b’s is different here, it is (ab)*, which will require no extra memory to be accepted. (Finite Automata can be built for this language). Hence L2 is regular language. Therefore Q is True.

  1. Consider the transition diagram of a PDA given below with input alphabet ∑ = {a, b} and stack alphabet Γ = {X, Z}. Z is the initial stack symbol. Let L denote the language accepted by the PDA.

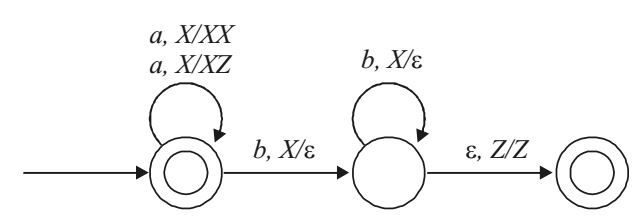
    Which one of the following is TRUE?








  1. View Hint View Answer Discuss in Forum

    Initial state is also the final state. So an is also accepted.

    Correct Option: D

    Initial state is also the final state. So an is also accepted.

  1. Consider the following context-free grammars:
    G1 : S → aS | B, B → b | bB
    G2 : S → aA | bB, A → aA | B | ε , B → bB | ε
    Which one of the following pairs of languages is generated by G1 and G2, respectively?








  1. View Hint View Answer Discuss in Forum

    In G1, there will be atleast 1 b because S->B and B->b. But no. of A's can be 0 as well and no. of A and B are independent. In G2, either we can take S->aA or S- >bB. So it must have atleast 1 a or 1 b. So option (d) is correct.

    Correct Option: D

    In G1, there will be atleast 1 b because S->B and B->b. But no. of A's can be 0 as well and no. of A and B are independent. In G2, either we can take S->aA or S- >bB. So it must have atleast 1 a or 1 b. So option (d) is correct.

  1. Which of the following decision problems are undecidable?
    I. Given NFAs N1 and N2, is L(N1) ∩ L(N2) = Φ ?
    II. Given a CFG G = (N, ∑ , P, S) and a string x ∈ ∑*, does x ∈ L(G) ?
    III. Given CFGs G1 and G2 is L(G1) = L(G2)?
    IV. Given a TM M, is L(M) = Φ ?








  1. View Hint View Answer Discuss in Forum

    There is no known algorithm to verify whether the language accepted by TM is empty or not. Similarly there is no algorithm to verify whether language of CFG’s are equivalent.

    Correct Option: C

    There is no known algorithm to verify whether the language accepted by TM is empty or not. Similarly there is no algorithm to verify whether language of CFG’s are equivalent.