Theory of computation miscellaneous Easy Questions and Answers

Theory of computation miscellaneous

Let L be the language represented by the regular expression

What is the minimum number of states in a DFA that recognizes L (complement of L)?

Correct Option: B

Consider the alphabet ∑ = {0, 1}, the null/empty string λ and the sets of strings X₀, X₁, and X₂ generated by the corresponding non-terminals of a regular grammar X₀, X₁, and X₂ are related as follows. X₀ = 1 X₁
X₁ = 0 X₁ + 1 X₂
X₂ = 0 X₁ + {λ}
Which one of the following choices precisely represents the strings in X₀ ?

Correct Option: C

The number of states in the minimal deterministic finite automata corresponding to the regular expression (0 + 1) * (10) is _______.

(0 +1)*10

K total minimum DFA states = 3

Correct Option: C

(0 +1)*10

K total minimum DFA states = 3

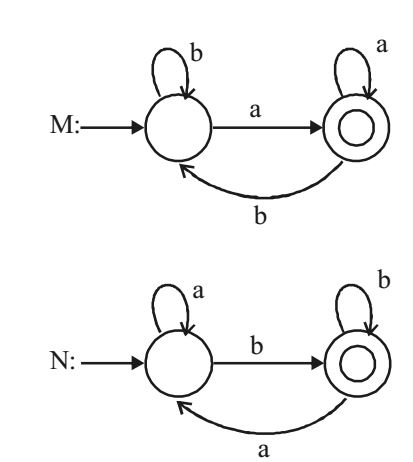
Consider the DFAs M and N given above. The number of states in a minimal DFA that accepts the languages L(M) ∩ L(N) is ________.

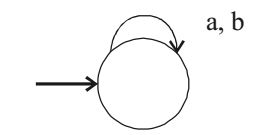
M accepts the strings which end with a and N accepts the strings which end with b. Their intersection should accept empty language.

Correct Option: A

M accepts the strings which end with a and N accepts the strings which end with b. Their intersection should accept empty language.

Consider the following two statements:
I. If all states of an NFA are accepting states then the language accepted by the NFA is ∑*.
II. There exists a regular language A such that for all languages B, A ∩ B is regular. Which one of the following is CORRECT?

Statement I is not true, because if all the states of DFA are accepting states then the language accepted by the DFA is * å Statement II is true because one can have regular language A = [] [Empty Language] which satisfies the given condition.