Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. Given below are two finite state automata ( → indicates the start state and F indicates a final state)

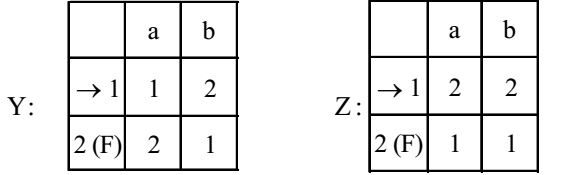
    Which of the following represents the product automata Z × Y?








  1. View Hint View Answer Discuss in Forum

    Given : Transition table for Y and Z
    The number of states of Z = 2
    The number of states of Y = 2
    Z × Y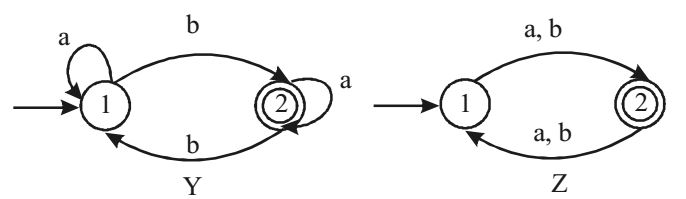

    No. of states of the product of Z and Y = 2 × 2 = 4
    Now, the states as per the given options are P, Q, R and S. The finite state automata is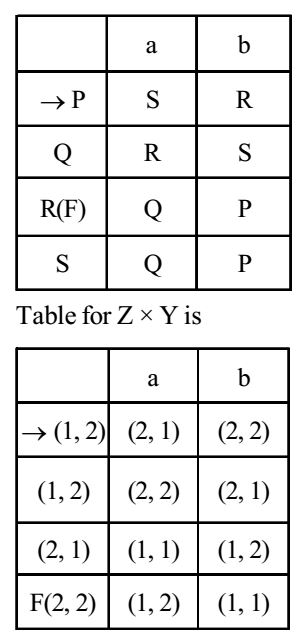

    Correct Option: A

    Given : Transition table for Y and Z
    The number of states of Z = 2
    The number of states of Y = 2
    Z × Y

    No. of states of the product of Z and Y = 2 × 2 = 4
    Now, the states as per the given options are P, Q, R and S. The finite state automata is

  1. Which of the following is true?









  1. View Hint View Answer Discuss in Forum

    Finite subset of non-regular set is regular as we know that Pumping Lemma can be applied on all the finite sets that states that all finite sets are regular. Infinite union of finite set is not regular because regular sets can never be closed under infinite union.

    Correct Option: B

    Finite subset of non-regular set is regular as we know that Pumping Lemma can be applied on all the finite sets that states that all finite sets are regular. Infinite union of finite set is not regular because regular sets can never be closed under infinite union.

  1. A minimum state deterministic finite automata accepting the language L = {W | W ∈ {0, 1}*, number of 0's and 1's in W are divisible by 3 and 5, respectively as.









  1. View Hint View Answer Discuss in Forum

    It is given that the 0's and 1's are divisible by 3 and 5 and we know that 3 and 5 do not have any factor other than themselves or 1 i.e., these cannot be further breakdown.
    Therefore, number of states = 3 × 5 = 15
    The schematic representation is as follows: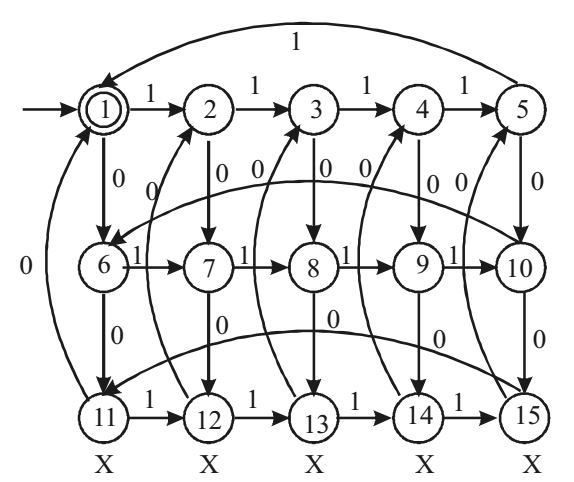

    Correct Option: A

    It is given that the 0's and 1's are divisible by 3 and 5 and we know that 3 and 5 do not have any factor other than themselves or 1 i.e., these cannot be further breakdown.
    Therefore, number of states = 3 × 5 = 15
    The schematic representation is as follows:

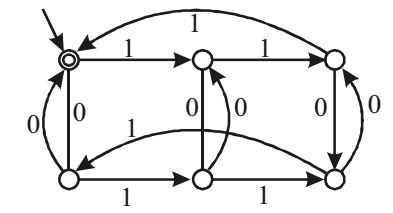
  1. The following finite state machine accepts all those binary strings in which the number of 1's and 0's are respectively.








  1. View Hint View Answer Discuss in Forum

    The given finite state machine accepts any string W ∈ (0, 1)* in which the number of 1's is multiple of 3 and the number of 0's is multiple of 2.

    Correct Option: A

    The given finite state machine accepts any string W ∈ (0, 1)* in which the number of 1's is multiple of 3 and the number of 0's is multiple of 2.

  1. The regular expression 0* (10)* denotes the same set as








  1. View Hint View Answer Discuss in Forum

    Option (a) solves to (1*0*)1*
    Option (b) solves to 0 + (0*1*0*)
    Option (c) solves to 0*1*10(0*1*)
    Therefore, none of the statement has the output equivalent to the given.

    Correct Option: D

    Option (a) solves to (1*0*)1*
    Option (b) solves to 0 + (0*1*0*)
    Option (c) solves to 0*1*10(0*1*)
    Therefore, none of the statement has the output equivalent to the given.