Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. Consider the following context-free grammar over the alphabet ∑ = {a, b, c} with S as the start symbol:
    S → abScT | abcT
    T → bT | b
    Which one of the following represents the language generated by the above grammar?








  1. View Hint View Answer Discuss in Forum

    The given context free Grammar
    ∑ = {a , b , c} with S as the start symbol.
    S → abScT/ abcT
    T → bT/ b
    The minimum length string generated by the grammar is 1.
    Consider first case ( S → abcT ) then ( S → abcb ) .
    Hence all the variable s are greater than 1.
    Consider second case
    S → abScT
    → ababScTcT
    → ababScTcTcT .............................. ..............................
    → (ab)n (CT)n
    Here T can generate any number of b's string with single b, so (T = bm)
    Hence, the language is
    L = [ (ab)n ( cbm )n | m , n ≥ 1 ]
    Hence option (c) is correct.

    Correct Option: C

    The given context free Grammar
    ∑ = {a , b , c} with S as the start symbol.
    S → abScT/ abcT
    T → bT/ b
    The minimum length string generated by the grammar is 1.
    Consider first case ( S → abcT ) then ( S → abcb ) .
    Hence all the variable s are greater than 1.
    Consider second case
    S → abScT
    → ababScTcT
    → ababScTcTcT .............................. ..............................
    → (ab)n (CT)n
    Here T can generate any number of b's string with single b, so (T = bm)
    Hence, the language is
    L = [ (ab)n ( cbm )n | m , n ≥ 1 ]
    Hence option (c) is correct.

  1. Let S and T be languages over ∑ = {a, b} represented by the regular expressions (a + b*)* and (a + b)*, respectively. Which of the following is true?








  1. View Hint View Answer Discuss in Forum

    Lets consider the regular expressions as given in the questions:

    Second, (a + b)*

    ⇒ (a + b*)* = (a + b*) Therefore, we can say that S = T

    Correct Option: C

    Lets consider the regular expressions as given in the questions:

    Second, (a + b)*

    ⇒ (a + b*)* = (a + b*) Therefore, we can say that S = T

  1. Consider a DFA over ∑ = {a, b} accepting all strings which have number of a's divisible by 6 and number of b's divisible by 8. What is the minimum number of states that the DFA will have?








  1. View Hint View Answer Discuss in Forum

    We construct a DFA for strings divisible by 6. It requires minimum 6 states as length of string mod 6 = 0, 1, 2, 3, 4, 5 We construct a DFA for strings divisible by 8. It requires minimum 8 states as length of string mod 8 = 0, 1, 2, 3, 4, 5, 6, 7 If first DFA is minimum and second DFA is also minimum then after merging both DFAs resultant DFA will also be minimum. Such DFA is called as compound automata. So, minimum states in the resultant DFA = 6 * 8 = 48 Thus, option (D) is the answer.

    Correct Option: D

    We construct a DFA for strings divisible by 6. It requires minimum 6 states as length of string mod 6 = 0, 1, 2, 3, 4, 5 We construct a DFA for strings divisible by 8. It requires minimum 8 states as length of string mod 8 = 0, 1, 2, 3, 4, 5, 6, 7 If first DFA is minimum and second DFA is also minimum then after merging both DFAs resultant DFA will also be minimum. Such DFA is called as compound automata. So, minimum states in the resultant DFA = 6 * 8 = 48 Thus, option (D) is the answer.

  1. Given an arbitrary Non-deterministic Finite Automata (NFA) with N states, the maximum number of states in an equivalent minimized DFA is at least








  1. View Hint View Answer Discuss in Forum

    In DFA any subset of the N states (for N element set N subsets possible) can become a new state and they can remain even when the DFA is minimized. So, maximum we can get N states for the minimized DFA.

    Correct Option: B

    In DFA any subset of the N states (for N element set N subsets possible) can become a new state and they can remain even when the DFA is minimized. So, maximum we can get N states for the minimized DFA.

  1. The smallest finite automata which accepts the language {x| length of x is divisible by 3} has








  1. View Hint View Answer Discuss in Forum

    Answer in the book is wrong

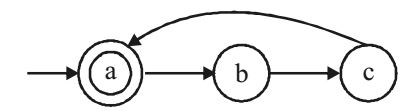
    Start & end are same as (a) hence the minimum no. of states required are3. Option (b) is correct. If string traversal doesn't stop at (a) then string length is not divisibleby 3.

    Correct Option: B

    Answer in the book is wrong

    Start & end are same as (a) hence the minimum no. of states required are3. Option (b) is correct. If string traversal doesn't stop at (a) then string length is not divisibleby 3.