Theory of computation miscellaneous Easy Questions and Answers | Page - 14

Theory of computation miscellaneous

Let L₁ , L₂ be any two context-free languages and R be any regular language. Then which of the following is/are CORRECT ?
I. L₁ ∪ L₂ is context-free.
II. L₁ is context-free.
III. L₁ – R is context-free.
IV. L₁ ∩ L₂ is context-free.

1. I , II and IV only
1. I and III only
1. II and IV only
1. I only

View Hint View Answer Discuss in Forum

1. L₁ ∪ L₂ is context-free because the union of two context free language is always a context free or CFL are closed under union operation. So, it is correct.
2. L₁ is not context-free because CFL are not closed under complement operation. So, it is incorrect.
3. L₁ - R is context-free because if context-free language is intersection to the complement of regular language then it is always context-free. L₁ - R = L₁ ∩ R₁, so it is correct.
4. L₁ ∩ L₂ is not context-free because context-free languages are not closed under complement operations. So it is incorrect.

Correct Option: B

1. L₁ ∪ L₂ is context-free because the union of two context free language is always a context free or CFL are closed under union operation. So, it is correct.
2. L₁ is not context-free because CFL are not closed under complement operation. So, it is incorrect.
3. L₁ - R is context-free because if context-free language is intersection to the complement of regular language then it is always context-free. L₁ - R = L₁ ∩ R₁, so it is correct.
4. L₁ ∩ L₂ is not context-free because context-free languages are not closed under complement operations. So it is incorrect.

Consider the following languages over the alphabet ∑ = {a, b, c}.
Let L₁ = { aⁿ bⁿ c^m | m , n ≥ 0 } and L₂ = { { a^m bⁿ cⁿ | m , n ≥ 0 }
Which of the following are context-free languages?
I. L₁ ∪ L₂
II. L₁ ∩ L₂

1. I only
1. II only
1. I and II
1. Neither I nor II

View Hint View Answer Discuss in Forum

The given language over Alphabets ∑ = (a, b, c) and the given language are :-
L₁ = { aⁿ bⁿ c^m | n , m ≥ 0 } is a CFL
L₂ = { a^m bⁿ cⁿ | n , m ≥ 0 } is also a CFL
then union of two CFL is always CFL,
L₁ ∪ L₂ = { aⁿ b^m c^k | (n = m) or (m = k), n , m ≥ 0 } is a context free language.
Intersection of two CFL is may or may not be a context free language.
L₁ ∩ L₂ = { aⁿ b^m c^k | (n = m) or (m = k) n , m ≥ 0 } or { aⁿ bⁿ cⁿ | n ≥ 0 } is a non context free language.
Hence, option (a) is correct.

Correct Option: A

The given language over Alphabets ∑ = (a, b, c) and the given language are :-
L₁ = { aⁿ bⁿ c^m | n , m ≥ 0 } is a CFL
L₂ = { a^m bⁿ cⁿ | n , m ≥ 0 } is also a CFL
then union of two CFL is always CFL,
L₁ ∪ L₂ = { aⁿ b^m c^k | (n = m) or (m = k), n , m ≥ 0 } is a context free language.
Intersection of two CFL is may or may not be a context free language.
L₁ ∩ L₂ = { aⁿ b^m c^k | (n = m) or (m = k) n , m ≥ 0 } or { aⁿ bⁿ cⁿ | n ≥ 0 } is a non context free language.
Hence, option (a) is correct.

Consider the following decision problems:
P₁. Does a given finite state machine accept a given string?
P₂. Does a given context-free grammar generate an infinite number of strings?
Which of the following statements is true?

1. Both P₁ and P₂ are decidable
1. Neither P₁ nor P₂ are decidable
1. Only P₁ is decidable
1. Only P₂ is decidable

View Hint View Answer Discuss in Forum

In P₁, A given finite state machine accepts a given string if it is decidable because in decidable problem there exists a turing machine that gives the correct answer for every statement in the domain of the problem. A class of problems with two outputs yes or no is said to be decidable (solvable), if there exist some definite algorithm which always terminates (halts) with one of the two outputs yes or no. Similarly, in P₂ , the context-free grammar generates.

Correct Option: A

In P₁, A given finite state machine accepts a given string if it is decidable because in decidable problem there exists a turing machine that gives the correct answer for every statement in the domain of the problem. A class of problems with two outputs yes or no is said to be decidable (solvable), if there exist some definite algorithm which always terminates (halts) with one of the two outputs yes or no. Similarly, in P₂ , the context-free grammar generates.

Let G = ({S}, {a, b}, R, S) be a context-free grammar where the rule set R is S → aSb | SS | ∈
Which of the following statements is true?

1. G is not ambiguous
1. There exist X, Y ∈ L(G) such that XY ∈ L(G)
1. There is a deterministic push-down automata that accepts L(G)
1. We can find a deterministic finite state automata that accepts L(G)

View Hint View Answer Discuss in Forum

The grammar is S → aSb | SS | ∈
(a) G is not ambiguous is false, since ∈ which belongs to L(G), has infinite number of derivation trees, which makes G ambiguous. Some derivation trees are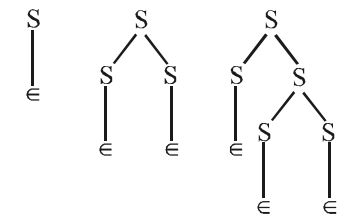

(b) There exists x, y ∈ L(G) such that xy ∉ L(G) is false, since S → SS, can be used derive xy, whenever x ∈ L(G) and y ∈ L(G).
(c) It is true, since this language is L(G) = { W | n_a (W) = n_b (W) and n_a (v) ≥ n_b (V) where V is any prefix of W }
This language happens to be deterministic context-free language.
∴ There exists a dpda that accepts it.
(d) It is false, as the given language is not regular.
∴ number of DFA exists to accept it.

Correct Option: C

The grammar is S → aSb | SS | ∈
(a) G is not ambiguous is false, since ∈ which belongs to L(G), has infinite number of derivation trees, which makes G ambiguous. Some derivation trees are

(b) There exists x, y ∈ L(G) such that xy ∉ L(G) is false, since S → SS, can be used derive xy, whenever x ∈ L(G) and y ∈ L(G).
(c) It is true, since this language is L(G) = { W | n_a (W) = n_b (W) and n_a (v) ≥ n_b (V) where V is any prefix of W }
This language happens to be deterministic context-free language.
∴ There exists a dpda that accepts it.
(d) It is false, as the given language is not regular.
∴ number of DFA exists to accept it.

Consider the following grammar G :
S → bS|aA|b
A → bA |aB
B → bB|aS| a
Let N_a (W) and N_b (W) denote the number of a 's and b 's in a string W respectively.
The language L(G) ⊆ {a, b}⁺ generated by G is

1. {W|N_a (W) > 3N_b (W)}
1. {W|N_b (W) > 3N_a (W)}
1. {W|N_a (W) = 3k, k ∈ {0, 1, 2,...}}
1. {W|N_b (W) = 3k, k ∈ {0, 1, 2,...}}

View Hint View Answer Discuss in Forum

Here, we have
S → bS
S → baA (S → aA)
S → baaB (A → aB)
S → baaa (B → a)
Therefore, | Na (w) | = 3.
Also, if we use A → bA instead of A → aB,
S → baA
S → babA
To terminate A, we would have to use A→ aB as only B terminates at a (B → a).
S → baA
S → babA
S → babaB
S → babaa
Thus, here also, | Na (w) | = 3. So, C is the correct answer.

Correct Option: C

Here, we have
S → bS
S → baA (S → aA)
S → baaB (A → aB)
S → baaa (B → a)
Therefore, | Na (w) | = 3.
Also, if we use A → bA instead of A → aB,
S → baA
S → babA
To terminate A, we would have to use A→ aB as only B terminates at a (B → a).
S → baA
S → babA
S → babaB
S → babaa
Thus, here also, | Na (w) | = 3. So, C is the correct answer.