Let G = ({S}, {a, b}, R, S) be a context-free grammar where

Home » Theory of Computation » Theory of computation miscellaneous » Question

Let G = ({S}, {a, b}, R, S) be a context-free grammar where the rule set R is S → aSb | SS | ∈
Which of the following statements is true?

1. G is not ambiguous
2. There exist X, Y ∈ L(G) such that XY ∈ L(G)
3. There is a deterministic push-down automata that accepts L(G)
4. We can find a deterministic finite state automata that accepts L(G)

Correct Option: C

The grammar is S → aSb | SS | ∈
(a) G is not ambiguous is false, since ∈ which belongs to L(G), has infinite number of derivation trees, which makes G ambiguous. Some derivation trees are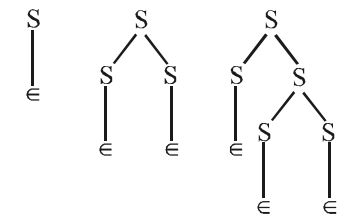

(b) There exists x, y ∈ L(G) such that xy ∉ L(G) is false, since S → SS, can be used derive xy, whenever x ∈ L(G) and y ∈ L(G).
(c) It is true, since this language is L(G) = { W | n_a (W) = n_b (W) and n_a (v) ≥ n_b (V) where V is any prefix of W }
This language happens to be deterministic context-free language.
∴ There exists a dpda that accepts it.
(d) It is false, as the given language is not regular.
∴ number of DFA exists to accept it.