Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. The finite state machine described by the following state diagram with A as starting state, where
    an arc label is
    x
    		 and x stands for 1-bit input and y stands for 2 bit output
    y









  1. View Hint View Answer Discuss in Forum

    As per the given diagram.

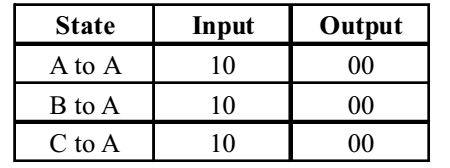
    Therefore, the finite state machine outputs the sum of the present and previous bits of the input.

    Correct Option: A

    As per the given diagram.

    Therefore, the finite state machine outputs the sum of the present and previous bits of the input.

  1. Consider the NFA, M, shown below:

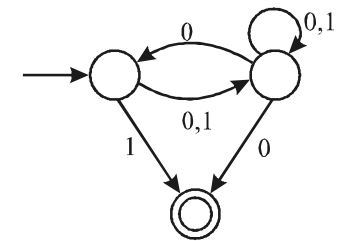
    Let the language accepted by M be L. Let L1 be the language accepted by the NFA M1 obtained by changing the accepting state of M to a non-accepting state and by changing the non-accepting state of M to accepting states. Which of the following statements is true?








  1. View Hint View Answer Discuss in Forum

    The given machine M is

    Now, the complementary machine M is

    In the case of DFA, L(M) = L(M) but in the case of nfa this is not true. Infact L(M) and L (M) have no connection.
    To find L1 = L(M), we have to look at M and directly find its language.
    Clearly, λ = L(M), since q0 is accepting it (0 + 1) (0 + 1)* ∈ L(M), since q2 is accepting it.
    ∴ L(M) = L1 = l + (0 + 1) (0 + 1)*
    ∴ L1 = (0 + 1)* = {0, 1}*

    Correct Option: B

    The given machine M is

    Now, the complementary machine M is

    In the case of DFA, L(M) = L(M) but in the case of nfa this is not true. Infact L(M) and L (M) have no connection.
    To find L1 = L(M), we have to look at M and directly find its language.
    Clearly, λ = L(M), since q0 is accepting it (0 + 1) (0 + 1)* ∈ L(M), since q2 is accepting it.
    ∴ L(M) = L1 = l + (0 + 1) (0 + 1)*
    ∴ L1 = (0 + 1)* = {0, 1}*

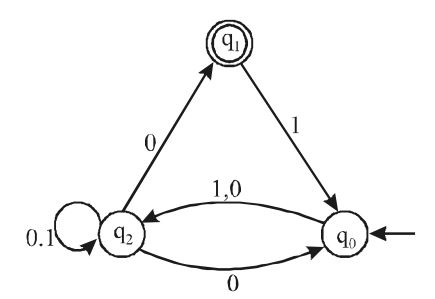
  1. Consider the following deterministic finite state automata M:
    Let S denotes the set of seven bit binary strings in which the first, the fourth and the last bits are 1. The number of strings in S that are accepted by M is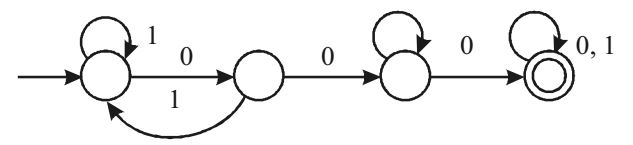








  1. View Hint View Answer Discuss in Forum

    The strings accepted by the given automata are of type.
    Option

    1 234 5 6 7
    1 ― ― 1 ― ― 1

    The four blank spaces can have a probability of having 0 or 1, so total 2(pow,4)= 16 strings are possible, but the given automata does not accept all of those.
    1. 1 1 1 1 0 0 1
    2. 1 1 0 1 0 0 1
    3. 1 0 1 1 0 0 1
    4. 1 0 0 1 0 0 1
    5. 1 0 0 1 0 0 1
    6. 1 0 0 1 1 0 1
    7. 1 0 0 1 1 1 1
    Hence (c) is correct option

    Correct Option: C

    The strings accepted by the given automata are of type.
    Option

    1 234 5 6 7
    1 ― ― 1 ― ― 1

    The four blank spaces can have a probability of having 0 or 1, so total 2(pow,4)= 16 strings are possible, but the given automata does not accept all of those.
    1. 1 1 1 1 0 0 1
    2. 1 1 0 1 0 0 1
    3. 1 0 1 1 0 0 1
    4. 1 0 0 1 0 0 1
    5. 1 0 0 1 0 0 1
    6. 1 0 0 1 1 0 1
    7. 1 0 0 1 1 1 1
    Hence (c) is correct option

  1. The regular expression 0* (10)* denotes the same set as








  1. View Hint View Answer Discuss in Forum

    Option (a) solves to (1*0*)1*
    Option (b) solves to 0 + (0*1*0*)
    Option (c) solves to 0*1*10(0*1*)
    Therefore, none of the statement has the output equivalent to the given.

    Correct Option: D

    Option (a) solves to (1*0*)1*
    Option (b) solves to 0 + (0*1*0*)
    Option (c) solves to 0*1*10(0*1*)
    Therefore, none of the statement has the output equivalent to the given.

  1. The following finite state machine accepts all those binary strings in which the number of 1's and 0's are respectively.








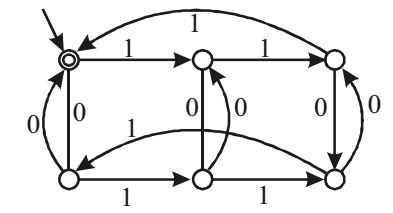
  1. View Hint View Answer Discuss in Forum

    The given finite state machine accepts any string W ∈ (0, 1)* in which the number of 1's is multiple of 3 and the number of 0's is multiple of 2.

    Correct Option: A

    The given finite state machine accepts any string W ∈ (0, 1)* in which the number of 1's is multiple of 3 and the number of 0's is multiple of 2.