Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. Let L1 = {w ∈ {0, 1}*| w has at least as many occurrences of (110)'s as (011)'s}. Let L2 = {w ∈ {0, 1}* | w has at least as many occurrences of (000)'s as (111)'s}. Which one of the following is TRUE?








  1. View Hint View Answer Discuss in Forum

    L1 is regular but L2 is not

    Correct Option: A

    L1 is regular but L2 is not

  1. Let ∑ be a finite non-empty alphabet and let 2∑* be the power set of ∑*. Which one of the following is TRUE?








  1. View Hint View Answer Discuss in Forum

    ∑* is countabily finite 2∑* is power set of ∑*
    The powerset of countabily infinite set is uncountable
    ∴ 2∑* is uncountable and ∑* is countable.

    Correct Option: C

    ∑* is countabily finite 2∑* is power set of ∑*
    The powerset of countabily infinite set is uncountable
    ∴ 2∑* is uncountable and ∑* is countable.

  1. The length of the shortest string NOT in the language (over ∑ = {a, b}) of the following regular expression is
    ______________.
    a*b* (ba)*a*








  1. View Hint View Answer Discuss in Forum

    a * b * (ba) * a *
    Length O is present (as it accepts ∈)
    Length 1 is present (a, b)
    Length 2 is present (aa, ab, ba, bb)
    Length 3 is not present (bab not present)
    ∴ it is 3

    Correct Option: B

    a * b * (ba) * a *
    Length O is present (as it accepts ∈)
    Length 1 is present (a, b)
    Length 2 is present (aa, ab, ba, bb)
    Length 3 is not present (bab not present)
    ∴ it is 3

  1. A deterministic finite automata (DFA)D with alphabet ∑ = {a, b} is given below.

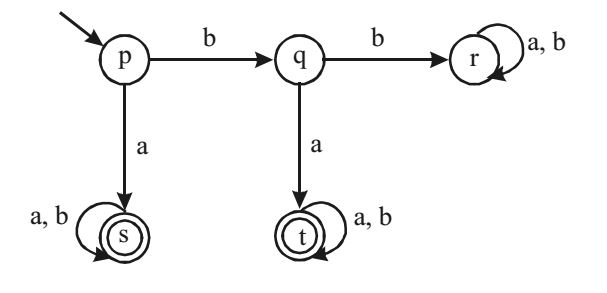
    Which of the following finite state machines is a valid minimal DFA which accepts the same language as D?








  1. View Hint View Answer Discuss in Forum

    As state (s) and (t) both are final states and accepting a* + b*, we can combine both states and we will get

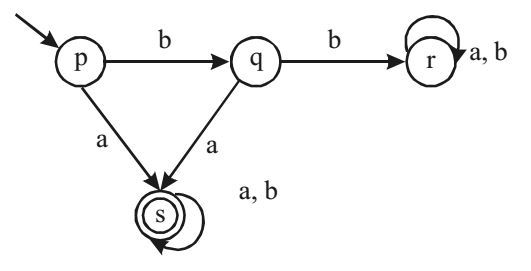
    Correct Option: A

    As state (s) and (t) both are final states and accepting a* + b*, we can combine both states and we will get

  1. Which of the following is true?









  1. View Hint View Answer Discuss in Forum

    Finite subset of non-regular set is regular as we know that Pumping Lemma can be applied on all the finite sets that states that all finite sets are regular. Infinite union of finite set is not regular because regular sets can never be closed under infinite union.

    Correct Option: B

    Finite subset of non-regular set is regular as we know that Pumping Lemma can be applied on all the finite sets that states that all finite sets are regular. Infinite union of finite set is not regular because regular sets can never be closed under infinite union.