Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. Consider the finite automata in the following figure.

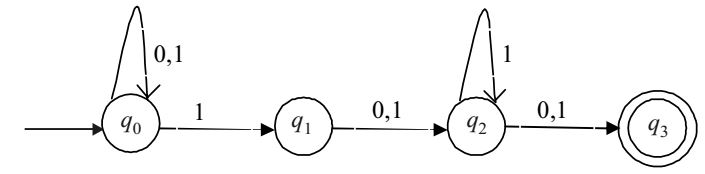
    Which is the set of reachable states for the input string 0011?








  1. View Hint View Answer Discuss in Forum

    Following paths can be taken by the finite Automata for the input string “0011”:––


    We note that no other path is possible for the input string "0011". So, finally union of all three cases gives us the set of Reachable states which is {q0, q1, q2}

    Correct Option: A

    Following paths can be taken by the finite Automata for the input string “0011”:––


    We note that no other path is possible for the input string "0011". So, finally union of all three cases gives us the set of Reachable states which is {q0, q1, q2}

  1. Which of the regular expressions given below represent the following DFA?

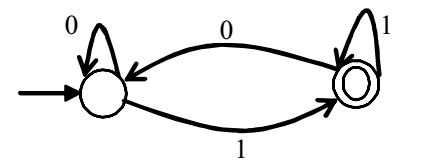
    I 0*1(1+00*1)*
    II 0*1*1+11*0*1
    III (0+1)*1








  1. View Hint View Answer Discuss in Forum

    (I) 0 *1(1 + 0 0 *1)*
    (II) 0 *1*1+11*0 *1
    (III) (0 +1)*1
    (I) and (III) represent DFA.
    (II) Doesn't represent as the DFA accepts strings like 11011, but the given regular expression doesn't accept.

    Correct Option: B

    (I) 0 *1(1 + 0 0 *1)*
    (II) 0 *1*1+11*0 *1
    (III) (0 +1)*1
    (I) and (III) represent DFA.
    (II) Doesn't represent as the DFA accepts strings like 11011, but the given regular expression doesn't accept.

  1. The length of the shortest string NOT in the language (over ∑ = {a, b}) of the following regular expression is
    ______________.
    a*b* (ba)*a*








  1. View Hint View Answer Discuss in Forum

    a * b * (ba) * a *
    Length O is present (as it accepts ∈)
    Length 1 is present (a, b)
    Length 2 is present (aa, ab, ba, bb)
    Length 3 is not present (bab not present)
    ∴ it is 3

    Correct Option: B

    a * b * (ba) * a *
    Length O is present (as it accepts ∈)
    Length 1 is present (a, b)
    Length 2 is present (aa, ab, ba, bb)
    Length 3 is not present (bab not present)
    ∴ it is 3

  1. A deterministic finite automata (DFA)D with alphabet ∑ = {a, b} is given below.

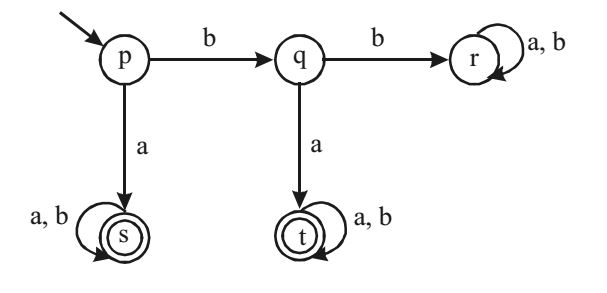
    Which of the following finite state machines is a valid minimal DFA which accepts the same language as D?








  1. View Hint View Answer Discuss in Forum

    As state (s) and (t) both are final states and accepting a* + b*, we can combine both states and we will get

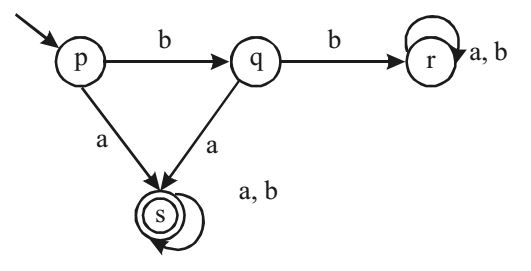
    Correct Option: A

    As state (s) and (t) both are final states and accepting a* + b*, we can combine both states and we will get

  1. Consider the alphabet ∑ = {0, 1}, the null/empty string λ and the sets of strings X0, X1, and X2 generated by the corresponding non-terminals of a regular grammar X0, X1, and X2 are related as follows. X0 = 1 X1
    X1 = 0 X1 + 1 X2
    X2 = 0 X1 + {λ}
    Which one of the following choices precisely represents the strings in X0 ?








  1. View Hint View Answer Discuss in Forum

    NA

    Correct Option: C

    NA