Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. S → aSa |bSb| a | b; The language generated by the above grammar over the alphabet {a, b} is the set of








  1. View Hint View Answer Discuss in Forum

    Given grammar S → aSabSbab. The strings generated through this grammar is definitely palindromes,but not all it can only generate palindromes of odd length only so (A) & (D) are false, (B) is correct. Also it can generate palindromes which start and end with same symbol, but not all strings eg. aabababba .

    Correct Option: B

    Given grammar S → aSabSbab. The strings generated through this grammar is definitely palindromes,but not all it can only generate palindromes of odd length only so (A) & (D) are false, (B) is correct. Also it can generate palindromes which start and end with same symbol, but not all strings eg. aabababba .

  1. Let L = {W ∈ (0, 1) * | W has even number of 1s}, i.e., L is the set of all bit strings with even number of 1's. Which one of the regular expressions below represents L?








  1. View Hint View Answer Discuss in Forum

    It is given that L is the set of all bit strings with even number of 1's so the regular expression should exhibit the same. Now, the min string should be e and the string should be e, 0, 11, 101,... The string obtained from such expression is 0* (10* 10 *)*

    Correct Option: B

    It is given that L is the set of all bit strings with even number of 1's so the regular expression should exhibit the same. Now, the min string should be e and the string should be e, 0, 11, 101,... The string obtained from such expression is 0* (10* 10 *)*

  1. Let W be any string of length n in {0, 1}*. Let L be the set of all sub-strings of W. What is the minimum number of states in a non-deterministic finite automata that accept L?








  1. View Hint View Answer Discuss in Forum

    L is the set of all substrings of w where w! {0,1}) Any string in L would have length 0 to n, with any no. of 1's and 0's The NDFA

    Here n = 4
    So to accept all the substrings the no. of states required are n + 1 = 4 + 1 = 5
    Hence (c) is correct option.

    Correct Option: C

    L is the set of all substrings of w where w! {0,1}) Any string in L would have length 0 to n, with any no. of 1's and 0's The NDFA

    Here n = 4
    So to accept all the substrings the no. of states required are n + 1 = 4 + 1 = 5
    Hence (c) is correct option.

  1. Definition of a language L with alphabet {a} is given as following and n is a positive integer constant. What is the minimum number of states needed in a DFA to recognize L?








  1. View Hint View Answer Discuss in Forum

    As n is constant atleast n + 1 states will required to design ank.

    Correct Option: B

    As n is constant atleast n + 1 states will required to design ank.

  1. A deterministic finite automata (DFA)D with alphabet ∑ = {a, b} is given below.

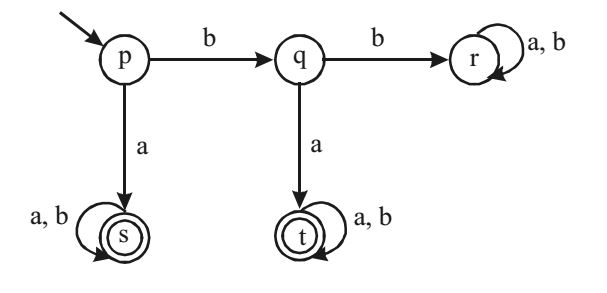
    Which of the following finite state machines is a valid minimal DFA which accepts the same language as D?








  1. View Hint View Answer Discuss in Forum

    As state (s) and (t) both are final states and accepting a* + b*, we can combine both states and we will get

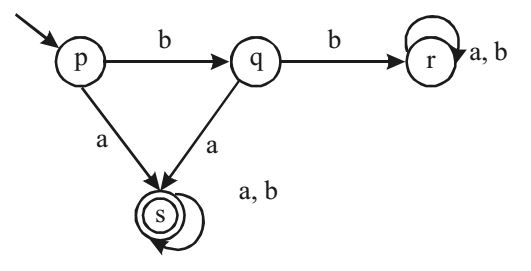
    Correct Option: A

    As state (s) and (t) both are final states and accepting a* + b*, we can combine both states and we will get