Theory of computation miscellaneous
- Let X be a recursive language and Y be a recursively enumerable but not recursive language. Let W and Z be two languages such that Y reduces to W, and Z reduces to X (reduction means the standard many-one reduction). Which one of the following statements is TRUE?
-
View Hint View Answer Discuss in Forum
NA
Correct Option: C
NA
- Which of the following languages is generated by the given grammar?
-
View Hint View Answer Discuss in Forum
NA
Correct Option: D
NA
- Consider the following languages.
L1 = {ap | p is a prime number}
L2 = {an bm c2m | n ≥ 0, m ≥ 0}
L3 = {an bn c2n | n ≥ 0}
L4 = {an bn | n ≥ 1}
Which of the following are CORRECT?
I. L1 is context-free but not regular.
II. L2 is not context-free.
III. L3 is not context-free but recursive.
IV. L4 is deterministic context-free.
-
View Hint View Answer Discuss in Forum
Consider the given languages.
L1 = {aP | P is a Prime Number},
L2 = 2 { an bm c2m | n ≥ 0 , m ≥ 0 }
L3 = 2 { an bn c2n | n ≥ 0 } , L4 = { an bn | n ≥ 1 } .
Now, consider each option:
(i) L1 is context free but not regular is Incorrect because it is not CFL, it is a CSL (Context sensitive language).
(ii) L2 is not CFL is also Incorrect because it is CFL.
(iii) L3 is not context free but recursive is correct because L3 is CSL (context sensitive language) and every CSL is recursive.
(iv) L4 is deterministic context free is correct because L4 is a proper subset of context free language. Hence option (d) is correct.Correct Option: D
Consider the given languages.
L1 = {aP | P is a Prime Number},
L2 = 2 { an bm c2m | n ≥ 0 , m ≥ 0 }
L3 = 2 { an bn c2n | n ≥ 0 } , L4 = { an bn | n ≥ 1 } .
Now, consider each option:
(i) L1 is context free but not regular is Incorrect because it is not CFL, it is a CSL (Context sensitive language).
(ii) L2 is not CFL is also Incorrect because it is CFL.
(iii) L3 is not context free but recursive is correct because L3 is CSL (context sensitive language) and every CSL is recursive.
(iv) L4 is deterministic context free is correct because L4 is a proper subset of context free language. Hence option (d) is correct.
- The minimum possible number of states of a deterministic finite automata that accepts the regular language L = {w1 aw2 | w1 ,w2 ∈ {a, b}*, | w1 | = 2, |w2 | ≥ 3} is ________.
-
View Hint View Answer Discuss in Forum
The Minimum possible number of states of deterministic finite Automata that accepts the regular language.
As given that,
L = { W1 a W2 | W1 , W2 ∈ {a , b}*, | W1 | = 2, | W2 | ≥ 3 } is
The regular expression for L is = (a + b)(a + b) a(a + b)(a + b)(a + b)(a + b )*
The minimal DFA accepting L is :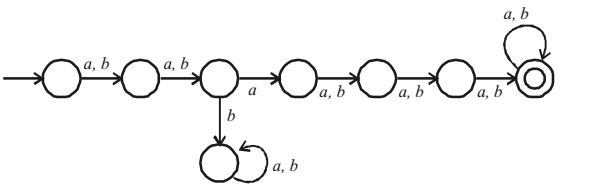
Hence, the minimum number of state are 8.Correct Option: B
The Minimum possible number of states of deterministic finite Automata that accepts the regular language.
As given that,
L = { W1 a W2 | W1 , W2 ∈ {a , b}*, | W1 | = 2, | W2 | ≥ 3 } is
The regular expression for L is = (a + b)(a + b) a(a + b)(a + b)(a + b)(a + b )*
The minimal DFA accepting L is :
Hence, the minimum number of state are 8.
- Identify the language generated by the following grammar, where S is the start variable.
S → XY
X → aX | a
Y → aYb | ∈
-
View Hint View Answer Discuss in Forum
The given grammar with S as start symbol is
S → XY
X → ax | a ⇒ X → ( am | m ≥ 1 )
Y → ayb | E ⇒ Y → ( an bn | n ≥ 0 )
S → XY
S → { am bn | m > n , n ≥ 0 }
because, from Non terminal X we can generate any number of a's including a single 'a' and from Y equal number of a's and b's.
Hence L = { am bn | m > n , n ≥ 0 }
m > n , because at least one will be attached on left of am bn . So, option (c) is correct.Correct Option: C
The given grammar with S as start symbol is
S → XY
X → ax | a ⇒ X → ( am | m ≥ 1 )
Y → ayb | E ⇒ Y → ( an bn | n ≥ 0 )
S → XY
S → { am bn | m > n , n ≥ 0 }
because, from Non terminal X we can generate any number of a's including a single 'a' and from Y equal number of a's and b's.
Hence L = { am bn | m > n , n ≥ 0 }
m > n , because at least one will be attached on left of am bn . So, option (c) is correct.

