Theory of computation miscellaneous

Theory of computation miscellaneous

Easy Questions

Theory of Computation

Theory of computation miscellaneous
  1. The number of states in the minimum sized DFA that accepts the language defined by the regular expression (0 + 1) * (0 + 1) (0 + 1)* is ________.








  1. View Hint View Answer Discuss in Forum


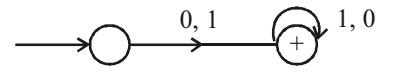
    So, the minimum number of states is 2.

    Correct Option: C


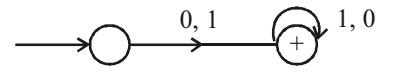
    So, the minimum number of states is 2.

  1. Which one of the following regular expressions represents the language: the set of all binary strings having two consecutive 0s and two consecutive 1s?








  1. View Hint View Answer Discuss in Forum

    Option (a) contains 00 and 11 consecutively which does not fulfill the required condition. Option (c) does not give assurance that both 00 and 11 will be exist in the string. According to option (d), string should start with 11 and ends with 00 or vice versa. Hence option (b) is the correct answer.

    Correct Option: B

    Option (a) contains 00 and 11 consecutively which does not fulfill the required condition. Option (c) does not give assurance that both 00 and 11 will be exist in the string. According to option (d), string should start with 11 and ends with 00 or vice versa. Hence option (b) is the correct answer.

  1. Let δ denote the transition function and d denote the extended transition function of the ∈-NFA whose transition table is given below:

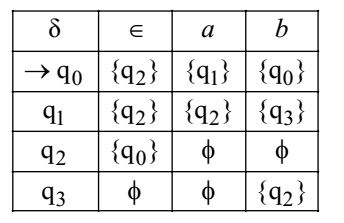
    Then d (q2, aba) is








  1. View Hint View Answer Discuss in Forum

    Converting the table to a state diagram then we get.

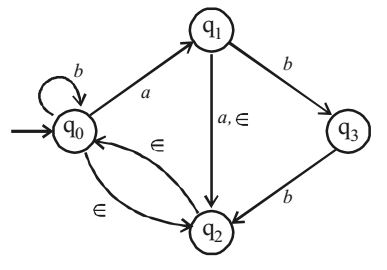
    then, δ̂= (q2 aba) All states reachable from q2 by aba.
    If aba is broken as ∈ , a , ∈ , ∈ , b , a then from q2 it can reach q1 and from there by null transaction to reach state q2 as well as q0.
    Consider, (q2 , a) = (q2 , ∈ a) = {q1 , q2 q0}.
    (q2 , ab) = (q1 , b) = {q0 , q3 , q2}
    (q2 , b) = {q0 , q2}
    (q0 , b) = {q0 , q2}
    (q2 , aba) = (q0 , a) = {q1 , q2 , q0}
    (q1 , a) = {q2 , q0}
    (q2 , a) = {q1 , q2 , q0}
    (q3 , a) = {q3}
    Then, δ̂= (q2 aba) = {q1 , q2 , q0}
    = {q0 , q1 , q2}
    Hence option (c) is correct.

    Correct Option: C

    Converting the table to a state diagram then we get.

    then, δ̂= (q2 aba) All states reachable from q2 by aba.
    If aba is broken as ∈ , a , ∈ , ∈ , b , a then from q2 it can reach q1 and from there by null transaction to reach state q2 as well as q0.
    Consider, (q2 , a) = (q2 , ∈ a) = {q1 , q2 q0}.
    (q2 , ab) = (q1 , b) = {q0 , q3 , q2}
    (q2 , b) = {q0 , q2}
    (q0 , b) = {q0 , q2}
    (q2 , aba) = (q0 , a) = {q1 , q2 , q0}
    (q1 , a) = {q2 , q0}
    (q2 , a) = {q1 , q2 , q0}
    (q3 , a) = {q3}
    Then, δ̂= (q2 aba) = {q1 , q2 , q0}
    = {q0 , q1 , q2}
    Hence option (c) is correct.

  1. Consider the language L given by the regular expression (a + b) *b (a + b) over the alphabet {a.b}. The smallest number of states needed in a deterministic finite-state automata (DFA) accepting L is ________.








  1. View Hint View Answer Discuss in Forum

    The given regular expression is (a + b) * b (a + b). In this all string whose second last bit is ‘b’. So, the minimal NFA is

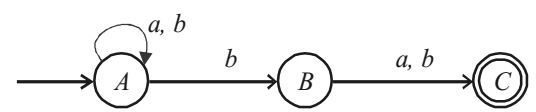
    It can be described as “All string over {a, b} ending with ‘ba’ or ‘bb’. Then the minimal (DFA) accepting (L), find by converting it into minimal DFA by subset construction Algorithm.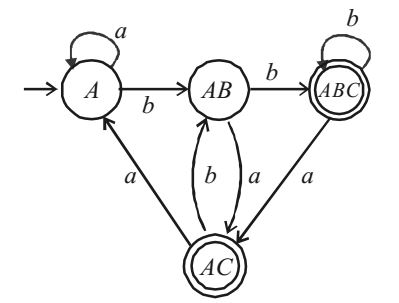

    Hence, it is a minimal DFA with 4 states.

    Correct Option: B

    The given regular expression is (a + b) * b (a + b). In this all string whose second last bit is ‘b’. So, the minimal NFA is

    It can be described as “All string over {a, b} ending with ‘ba’ or ‘bb’. Then the minimal (DFA) accepting (L), find by converting it into minimal DFA by subset construction Algorithm.

    Hence, it is a minimal DFA with 4 states.