-
Consider the NFA, M, shown below:
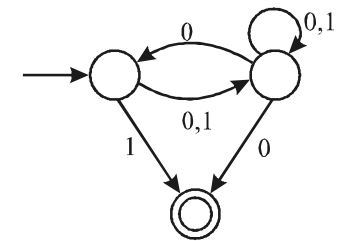
Let the language accepted by M be L. Let L1 be the language accepted by the NFA M1 obtained by changing the accepting state of M to a non-accepting state and by changing the non-accepting state of M to accepting states. Which of the following statements is true?
-
- L1 = {0, 1}* − L
- L1 = {0, 1}*
- L1 ⊆ 1
- L1 = L
- L1 = {0, 1}* − L
Correct Option: B
The given machine M is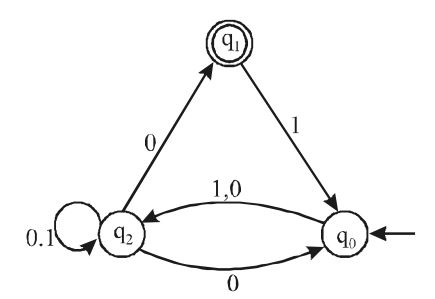
Now, the complementary machine M is
In the case of DFA, L(M) = L(M) but in the case of nfa this is not true. Infact L(M) and L (M) have no connection.
To find L1 = L(M), we have to look at M and directly find its language.
Clearly, λ = L(M), since q0 is accepting it (0 + 1) (0 + 1)* ∈ L(M), since q2 is accepting it.
∴ L(M) = L1 = l + (0 + 1) (0 + 1)*
∴ L1 = (0 + 1)* = {0, 1}*

