We find LCM of 63, 70 and 77 cm.

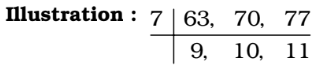
Required distance = LCM of 63, 70 and 77 cm.

Correct Option: C

We find LCM of 63, 70 and 77 cm.

∴ LCM = 7 × 9 × 10 × 11 = 6930
Required distance = LCM of 63, 70 and 77 cm. = 6930

As we know that When a number is divided by a, b or c leaving same remainder ‘r’ in each case then that number must be k + r where k is LCM of a, b and c.
Required number = (LCM of 15, 20, 36 and 48) + 3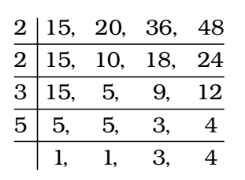

∴ LCM ( k ) = 2 × 2 × 3 × 5 × 3 × 4 = 720

Correct Option: D

As we know that When a number is divided by a, b or c leaving same remainder ‘r’ in each case then that number must be k + r where k is LCM of a, b and c.
Required number = (LCM of 15, 20, 36 and 48) + 3

∴ LCM ( k ) = 2 × 2 × 3 × 5 × 3 × 4 = 720
Here , r = 3
∴ Required number = k + r = 720 + 3 = 723

We know that Greatest n digit number which when divided by three numbers p,q,r leaves no remainder will be Required Number = (n – digit greatest number) – R , R is the remainder obtained on dividing greatest n digit number by L.C.M of p.q,r.
LCM of 10, 15 and 20 = 60
Largest 4-digit number = 9999

Correct Option: B

We know that Greatest n digit number which when divided by three numbers p,q,r leaves no remainder will be Required Number = (n – digit greatest number) – R , R is the remainder obtained on dividing greatest n digit number by L.C.M of p.q,r.
LCM of 10, 15 and 20 = 60
Largest 4-digit number = 9999

∴ Required number = 9999 – remainder = 9999 – 39 = 9960

The LCM of 6, 12 and 18 = 36 = 6²

Correct Option: D

The LCM of 6, 12 and 18 = 36 = 6² = 36
Hence , required answer is 36.

We find LCM of 20, 28, 32 and 35

∴ LCM = 2 × 2 × 5 × 7 × 8 = 1120
∴ Required number = 5834 – LCM of 20, 28, 32 and 35

Correct Option: B

We find LCM of 20, 28, 32 and 35

∴ LCM = 2 × 2 × 5 × 7 × 8 = 1120
∴ Required number = 5834 – LCM of 20, 28, 32 and 35
∴ Required number = 5834 – 1120 = 4714