-
Find the least number which when divided separately by 15, 20, 36 and 48 leaves 3 as remainder in each case.
-
- 183
- 243
- 483
- 723
Correct Option: D
As we know that When a number is divided by a, b or c leaving same remainder ‘r’ in each case then that number must be k + r where k is LCM of a, b and c.
Required number = (LCM of 15, 20, 36 and 48) + 3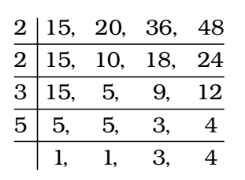
∴ LCM ( k ) = 2 × 2 × 3 × 5 × 3 × 4 = 720
Here , r = 3
∴ Required number = k + r = 720 + 3 = 723

