LCM and HCF
- A farmer has 945 cows and 2475 sheep. He farms them into flocks, keeping cows and sheep separate and having the same number of animals in each flock. If these flocks are as large as possible, then the maximum number of animals in each flock and total number of flocks required for the purpose are respectively
-
View Hint View Answer Discuss in Forum
First of all we find the HCF of 945 and 2475. HCF = 45
Illustration :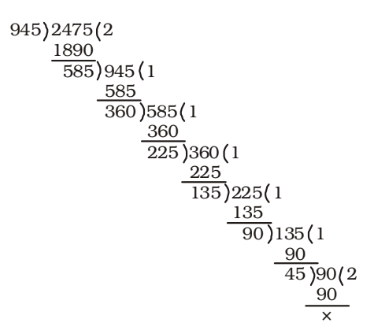
∴ Maximum number of animals in each flock = 45Required total number of flocks = 945 + 2475 45 45 Correct Option: C
First of all we find the HCF of 945 and 2475. HCF = 45
Illustration :
∴ Maximum number of animals in each flock = 45Required total number of flocks = 945 + 2475 = 21 + 55 = 76 45 45
- Three sets of English, Mathematics and Science books containing 336, 240, 96 books respectively have to be stacked in such a way that all the books are stored subject-wise and the height of each stack is the same. Total number of stacks will be
-
View Hint View Answer Discuss in Forum
Number of books in each stack = HCF of 336, 240, 96 = 48

∴ Total number of stacks = 336 + 240 + 96 48 48 48
Correct Option: A
Number of books in each stack = HCF of 336, 240, 96 = 48

∴ Total number of stacks = 336 + 240 + 96 48 48 48
Hence , Total number of stacks = 7 + 5 + 2 = 14
- The least number which when divided by 5, 6, 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder is
-
View Hint View Answer Discuss in Forum
The LCM of 5, 6, 7 and 8 = 840
∴ Required number = 840k + 3 , which is exactly divisible by 9 for some value of k.
Now, 840k + 3 = 93 × 9k + (3k + 3)
When k = 2 , 3k + 3 = 9, which is divisible by 9.
∴ Required number = 840k + 3Correct Option: B
The LCM of 5, 6, 7 and 8 = 840
∴ Required number = 840k + 3 , which is exactly divisible by 9 for some value of k.
Now, 840k + 3 = 93 × 9k + (3k + 3)
When k = 2 , 3k + 3 = 9, which is divisible by 9.
∴ Required number = 840k + 3 = 840 × 2 + 3 = 1683
- A milkman has 75 litres milk in one can and 45 litres in another. The maximum capacity of container which can measure milk of either container exact number of times is :
-
View Hint View Answer Discuss in Forum
Required maximum capacity of container = HCF of 75L and 45L
Now, 75 = 5 × 5 × 3
45 = 5 × 3 × 3
∴ HCF = 15Correct Option: C
Required maximum capacity of container = HCF of 75L and 45L
Now, 75 = 5 × 5 × 3
45 = 5 × 3 × 3
∴ HCF = 15
Required maximum capacity of container = 15 litres
- What is the greatest number which will divide 110 and 128 leaving a remainder 2 in each case ?
-
View Hint View Answer Discuss in Forum
As we know that the largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by H.C.F. of (a – p), (b – q) and (c – r).
Required number = HCF of (110 – 2) and (128 – 2)
Correct Option: B
As we know that the largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by H.C.F. of (a – p), (b – q) and (c – r).
Required number = HCF of (110 – 2) and (128 – 2)
Required number = HCF of 108 and 126 = 18

