Height and Distance
- A man 2 m high, walks at a uniform speed of 6 m/min away from a lamp post, 5 m high. Find the rate at which the length of his shadow increases .
-
View Hint View Answer Discuss in Forum
Let us draw a figure as per given question.
Let AB = 5 m and CD = 2 m be the heights of a lamp post and the men respectively. At any time t BD = x meter and shadow of man ED = y meter.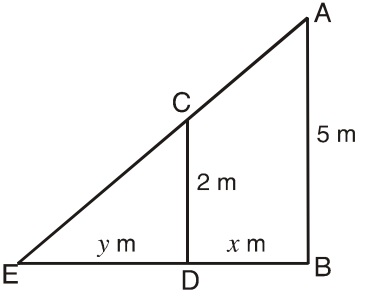
Correct Option: A
Let us draw a figure as per given question.
Let AB = 5 meter and CD = 2 meter be the heights of a lamp post and the men respectively.
At any time t BD = x meter and shadow of man ED = y meter.
Then, dx/dt = 6 m/min
Now, right triangles ABE and CDE are similar, then
AB/CD = BE/DE
⇒ 5/2 = (x + y)/y
⇒ 5y = 2x + 2y
⇒ 5y - 2y = 2x
⇒ 3y = 2x
⇒ 3 dy/dt = 2 dx/dt
⇒ 3 dy/dt = 2 x 6
⇒ dy/dt = 2 x 6 / 3
∴ dy/dt = 2 x 2 = 4
Hence, length of his shadow increase at the rate of 4 m/min.
- An observer measures angles of elevation of two tower of equal height from a point between the towers. If the angles of elevation are 60° and 30° and distance of nearer tower is 100 m then the height of each tower and the distance between the towers, respectively are
-
View Hint View Answer Discuss in Forum
Let us draw a figure below as per given question.
Let AB = CD = h meter be the heights of the towers. E is a point such that DE = 100 meter;
∠CED = 60° and ∠AEB = 30°
Now, BE = x meter (say)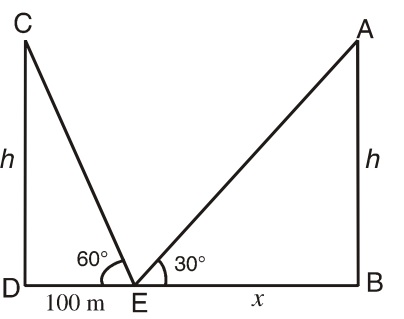
Correct Option: B
Let us draw a figure below as per given question.
Let AB = CD = h meter be the heights of the towers. E is a point such that DE = 100 meter;
∠CED = 60° and ∠AEB = 30°
Now, BE = x meter (say)
From right triangle CDE.
h = 100 tan 60°
⇒ h = 100√3 meter
From right triangle ABE,
x = h cot 30° put the value of h, we will get
x = 100√3 X √3
x = 100 X 3 = 300 meters
Distance between the tower = DE + EB = 100 + 300 = 400 meters
Height of the tower = h = 100√3 meter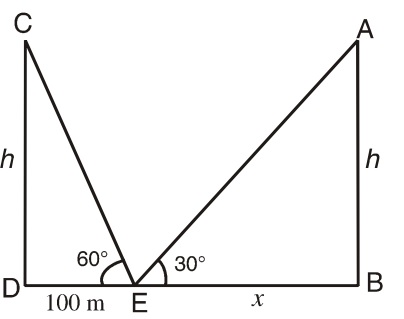
- A man on the top of a vertical towers observes a car moving at a uniform speed coming directly towards it. if it takes 12 minute for the angle of depression to change from 30° to 45°, how soon after this will the car reach the tower ?
-
View Hint View Answer Discuss in Forum
Let us draw a figure below from given question.
Let AB = h meter be the height of the tower B and C are two points such that ∠ACB = 30° ∠ADB = 45° and CD = x meter (say)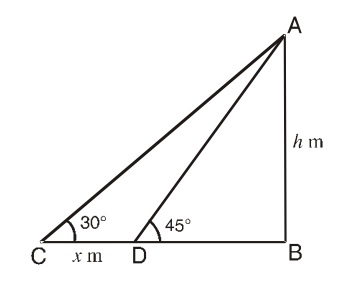
Correct Option: D
Let us draw a figure below from given question.
Let AB = h meter be the height of the tower B and C are two points such that ∠ACB = 30° ∠ADB = 45° and CD = x meter (say)
From right triangle ABD,
tan 45° = h/BD
∴ BD = h meter;
Again from right triangle ABC
tan 30° = h/(h + x )
⇒ h + x = √3 h
∴ x = (1.73 - 1)h = 0.73h
Now, 0.73h meter covered in 12 min
Hence, h meter covered in 12/0.73 = 1200/73 min = 16 min 23 sec .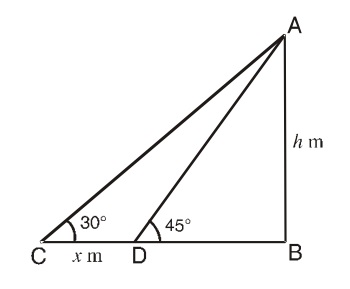
- The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance a towards the foot of the tower, the angle of elevation is found to be β. The height of the tower is :
-
View Hint View Answer Discuss in Forum
Let OP be the tower of height h (say) and A and B be the two positions on the horizontal line through O, such that
∠OAP = α, ∠OBP = β and assume that distance OB = x
As we draw the figure below as per given question and use the trigonometry formula and solve the question.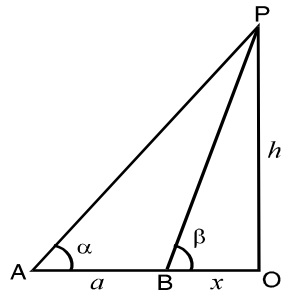
Correct Option: A
Let OP be the tower of height h (say) and A and B be the two positions on the horizontal line through O, such that
∠OAP = α, ∠OBP = β and OB = x
In ΔOBP, Use the trigonometry formula
Tanβ = P/B = Perpendicular distance / Base distance
Tanβ = OP/OB
⇒ OB = OP/Tanβ
⇒ OB = OP Cotβ
Put the value of OB and OP , We will get
x = h Cot β...............(1)
In ΔOAP, Similarly
Tanα = OP/OA
⇒ OA = OP/ Tanα
⇒ OA = OP Cot α
Put the value of OA and OP
⇒ a + x = h Cot α
⇒ x = h Cot α - a ............(2)
From equation (1) and (2)
∴ h Cot β = h Cot α - a
⇒ a = h Cot α - h Cot β
⇒ a = h (Cot α - Cot β)
⇒ a = h (Cos α/ Sin α - Cos β / Sin β )
⇒ a = h( (Cos α Sin β - Cos β Sin α ) /Sin α Sin β )
⇒ a = h( Sin(β - α) / Sin α Sin β)
⇒ h = a Sin α Sin β/ Sin(β - α)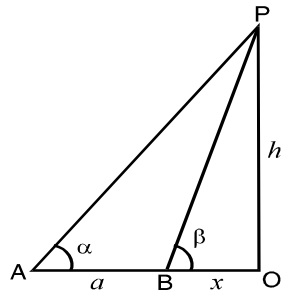
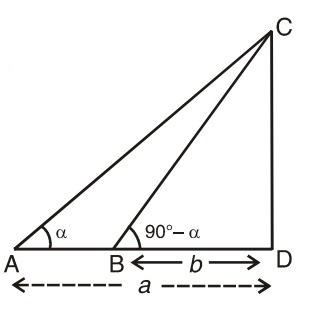
- The angles of elevation of the top of a verticle tower from two points, distance a and b (a > b) from the base and in the same straight line with it are complementary. Then the height of the tower is ?
-
View Hint View Answer Discuss in Forum
Let us draw a figure below as per given question.
Let CD = h unit be the height of the tower and A and B be the two points on the ground, such that DA = a; DB = b;
∠ DAC = ∝ and ∠DBC = 90° - ∝
Correct Option: A
Let CD = h unit be the height of the tower and A and B be the two points on the ground, such that DA = a; DB = b;
∠ DAC = ∝ and ∠DBC = 90° - ∝
From right triangle ADC, CD = h = a tan ∝ ...(i)
From right triangle BDC, CD = h = b tan (90° - ∝ ) = b cot ∝ .......(ii)
Multiplying equations (i) and (ii), we get
h2 = a tan ∝ X b cot∝
Hence, h = √ab