Height and Distance
- From the top of h meter high cliff the angles of depression of the top and the button of a tower are observed to be 30° and 60° respectively. The height of the tower is ?
-
View Hint View Answer Discuss in Forum
Let us draw a figure below as per given question.
Let AB = h meter be the height of cliff and CD = x m be the height of the tower and also ∠ ADB = 60° and ∠ACE = 30° ,
Correct Option: D
Let us draw a figure below as per given question.
Let AB = h meter be the height of cliff and CD = x meter be the height of the tower and also ∠ ADB = 60° and ∠ACE = 30° ,
Now, from the figure, AE = (h - x) meter
From right triangle ABD, BD = h cot 60° = h/√3 m
From right triangle CEA. (h - x) = EC tan 30° = BD tan 30°
⇒ h - x = h/√3 X 1/√3
∴ x = h - h/3 = 2h/3 meter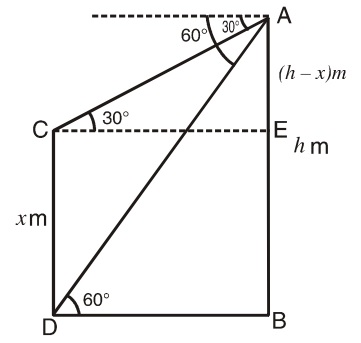
- A 20 m high electric pole stands upright on the ground with the help of steel wire to its top and affixed on the ground. If the steel wire makes 60° with the horizontal ground, then find out the length of the steel wire.
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
In triangle POQ , we have
PQ = 20 msin60° = PQ ⇒ √3 = 20 OP 2 OP 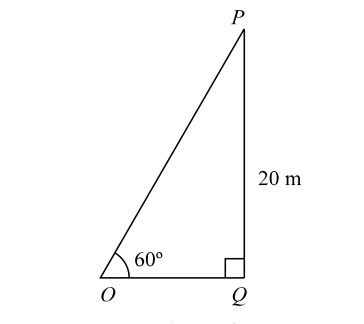
Correct Option: A
Let us draw the figure from the given question.
In triangle POQ , we have
PQ = 20 msin60° = PQ ⇒ √3 = 20 OP 2 OP ⇒ OP = 20 X 2 = 40 m. √2 √3 Hence ,The length of the steel wire = 40 m √3 
- The shadow of a tower standing on a level plane is found to be 50 m longer when the sun’s altitude is 30° than when it is 60°. Find the height of the tower.
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, T be the top of the tower AT. Let, AT = h m. Let, AB and AC be the shadows of the tower when the sun's altitude is 60° and 30°, respectively.
Correct Option: C
Let us draw the figure from the given question.
Let, T be the top of the tower AT. Let, AT = h m. Let, AB and AC be the shadows of the tower when the sun’s altitude is 60° and 30°, respectively.
Then, BC = 50m. Let, AB = x m.In figure TBA , cot 60° = AB AT ⇒ x = cot60° ⇒ x = h ........(1) h √3
∴ AC = AB + AC = 50 + hIn figure TCA , cot 30° = AC AT ⇒ x + 50 = cot30° ⇒ x + 50 = √3 h .......( 2 ) h
Subtracting Equation (1) from Equation (2),50 = 
√3 - 1 
h ⇒ h = 25 √3 m. √3
Hence , the height of the tower is 25 √3 m.
- A pole being broken by the wind, the top struck the ground at an angle of 30° and at a distance of 21 m from the foot of the pole. Find out the total height of the pole.
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, OAP be the pole. When broken by wind at A, let its top P strike the ground at P' so that OP' = 21 m, ∠OP'A = 30°, AP = AP'.
Correct Option: B
Let us draw the figure from the given question.
Let, OAP be the pole. When broken by wind at A .
let its top P strike the ground at P' so that OP' = 21 m, ∠OP'A = 30°, AP = AP'.
∴ OA = 7√3We have, tan 30° = OA ⇒ OA = 21 OP' √3  ∴ tan30° =
∴ tan30° = 1 
√3 Also, AP' = sec 30° ⇒ AP = 2 [ ∴ AP = AP' ] OP' 21 √3 ∴ AP = 42 = 14√3 ⇒ AP = 14√3. √3
Height of the pole = OP = OA + AP = 7√3 + 14√3 = 21√3.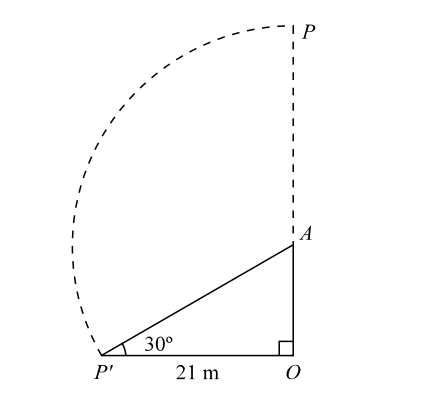
- The angle of elevation of moon when the length of the shadow of a pole is equal to its height, is:
-
View Hint View Answer Discuss in Forum
As per given question, we can draw a figure below.
According to question ,
The length of the shadow of a pole is equal to its height.
Let, Height of a pole AB = x.
Then, The length of the shadow of a pole AC = x.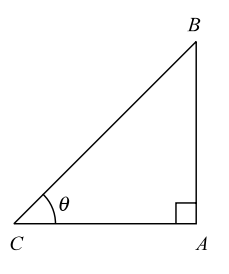
Correct Option: B
Let us draw the figure from the given question.
Given :- The length of the shadow of a pole is equal to its height.
Let, Height of a pole AB = x.
Then, The length of the shadow of a pole AC = x.In triangle ACB , tanθ = AB AC ∴ tanθ = x = 1 x
⇒ tanθ = tan45°
⇒ θ = 45°
Hence ,The angle of elevation of moon is 45° .

