-
From the top of h meter high cliff the angles of depression of the top and the button of a tower are observed to be 30° and 60° respectively. The height of the tower is ?
-
- h√3
- 2h√3
- h/3
- 2h/3
Correct Option: D
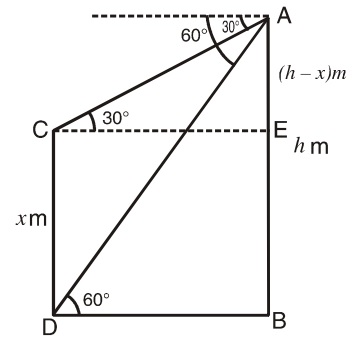
Let us draw a figure below as per given question.
Let AB = h meter be the height of cliff and CD = x meter be the height of the tower and also ∠ ADB = 60° and ∠ACE = 30° ,
Now, from the figure, AE = (h - x) meter
From right triangle ABD, BD = h cot 60° = h/√3 m
From right triangle CEA. (h - x) = EC tan 30° = BD tan 30°
⇒ h - x = h/√3 X 1/√3
∴ x = h - h/3 = 2h/3 meter