-
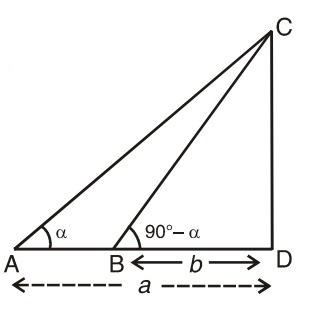
The angles of elevation of the top of a verticle tower from two points, distance a and b (a > b) from the base and in the same straight line with it are complementary. Then the height of the tower is ?
-
- √(ab)
- √(a2 + b2)
- √(a2 - b2)
- √a(a - b)
- ..
Correct Option: A
Let CD = h unit be the height of the tower and A and B be the two points on the ground, such that DA = a; DB = b;
∠ DAC = ∝ and ∠DBC = 90° - ∝
From right triangle ADC, CD = h = a tan ∝ ...(i)
From right triangle BDC, CD = h = b tan (90° - ∝ ) = b cot ∝ .......(ii)
Multiplying equations (i) and (ii), we get
h2 = a tan ∝ X b cot∝
Hence, h = √ab