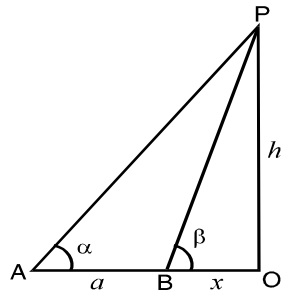
-
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance a towards the foot of the tower, the angle of elevation is found to be β. The height of the tower is :
-
- a Sin α Sin β/ Sin(β - α)
- a Sin α Sin β/Sin(α - β)
- a Sin( β - α ) Sin α Sin β
- a Sin(α - β)/Sin αSin β
Correct Option: A
Let OP be the tower of height h (say) and A and B be the two positions on the horizontal line through O, such that
∠OAP = α, ∠OBP = β and OB = x
In ΔOBP, Use the trigonometry formula
Tanβ = P/B = Perpendicular distance / Base distance
Tanβ = OP/OB
⇒ OB = OP/Tanβ
⇒ OB = OP Cotβ
Put the value of OB and OP , We will get
x = h Cot β...............(1)
In ΔOAP, Similarly
Tanα = OP/OA
⇒ OA = OP/ Tanα
⇒ OA = OP Cot α
Put the value of OA and OP
⇒ a + x = h Cot α
⇒ x = h Cot α - a ............(2)
From equation (1) and (2)
∴ h Cot β = h Cot α - a
⇒ a = h Cot α - h Cot β
⇒ a = h (Cot α - Cot β)
⇒ a = h (Cos α/ Sin α - Cos β / Sin β )
⇒ a = h( (Cos α Sin β - Cos β Sin α ) /Sin α Sin β )
⇒ a = h( Sin(β - α) / Sin α Sin β)
⇒ h = a Sin α Sin β/ Sin(β - α)