Height and Distance
- The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electric pole and an angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, AB be the tower and CD be the electric pole.
Let, BC = DE = x.
Given :- AB = 15 m
Correct Option: C
Let us draw the figure from the given question.
Let, AB be the tower and CD be the electric pole.
Let, BC = DE = x.
Given :- AB = 15 mNow In triangle ACB ; we have , AB = tan60° . BC ⇒ 15 = √3 ⇒ x = 15 . x √3 Also ; In triangle ADE , AE = tan30° DE ⇒ y = 1 15/√3 √3
⇒ 3y = 15 ⇒ y = 5∴ CD = BE = AB - AE = 15 - 5 = 10 m.
Hence , the height of the electric pole is 10 m .
- The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle 30° with the horizontal, then the length of the wire is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let the length of the wire is l .
Given :- QT = 6 m and RT = 14 m
In figure , we have6 = sin 30° = 1 l 2 
Correct Option: A
Let us draw the figure from the given question.
Let the length of the wire is l .
Given :- QT = 6 m and RT = 14 m
In figure , we have6 = sin 30° = 1 l 2 ⇒ l = 12 m.
Hence , the length of the wire is 12 m .
- The angle of elevation of the sun when the length of the shadow of a pole is √3 times the height of the pole will be :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Given, AC = √3 AB ......... ( 1 )
and ∠BCA = θ .
Correct Option: A
Let us draw the figure from the given question.
Given, AC = √3 AB ......... ( 1 )
and ∠BCA = θ .
In triangle ACB , we have∴ cot θ = AC = √3 ⇒ tan θ = 1 [ From equation ( 1 ) ] AB √3 ⇒ tan θ = tan 30° ⇒ θ = 30°. 
- A tower subtends an angle of 30° at a point on the same level as the foot of the tower. At a second point, h m above the first, the depression of the foot of the tower is 60°. The horizontal distance of the tower from the point is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, PQ = x m denote the tower, so that ∠PAQ = 30°. Let, BA = h m.
∴ ∠BQA = 60°.
Correct Option: A
Let us draw the figure from the given question.
Let, PQ = x m denote the tower, so that ∠PAQ = 30°. Let, BA = h m.
∴ ∠BQA = 60°.
In triangle BQA , we havetan60°= AB AQ ⇒ h = tan60° = √3. AQ ∴ AQ = h = h cot60°. √3
Hence , the horizontal distance of the tower from the point is h cot60° .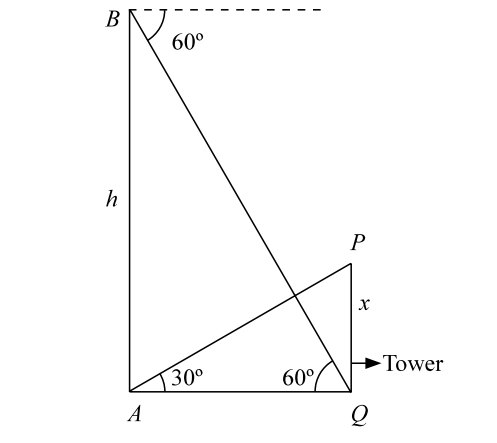
- At a point, 15 m away from the base of a 15 m high house, the angle of elevation of the top is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, MP denote the house. Let, θ be the angle of elevation.
Correct Option: A
Let us draw the figure from the given question.
Let, MP denote the house. Let, θ be the angle of elevation.∴ tanθ = MP = 15 = 1. OM 15 ∴ θ = 45° . 

