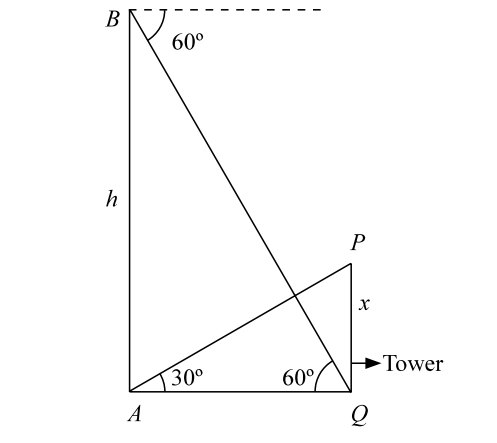
-
A tower subtends an angle of 30° at a point on the same level as the foot of the tower. At a second point, h m above the first, the depression of the foot of the tower is 60°. The horizontal distance of the tower from the point is :
-
- h cot 60°
- h cot 30°
-
h cot 60° 2 -
h cot 30° 2
Correct Option: A
Let us draw the figure from the given question.
Let, PQ = x m denote the tower, so that ∠PAQ = 30°. Let, BA = h m.
∴ ∠BQA = 60°.
In triangle BQA , we have
| tan60°= | AB |
| AQ |
| ⇒ | h | = | tan60° | = √3. |
| AQ |
| ∴ AQ | = | h | = h cot60°. |
| √3 |
Hence , the horizontal distance of the tower from the point is h cot60° .