Ratio, Proportion
- A’s income is Rs. 140 more than B’s income and C’s income is Rs. 80 more than D’s. If the ratio of A’s and C’s incomes is 2 : 3 and the ratio of B’s and D’s incomes is 1 : 2, then the incomes of A, B, C and D are respectively
-
View Hint View Answer Discuss in Forum
Let A‘s income be Rs. 2x.
∴ B’s income = Rs. (2x – 140)
C’s income = Rs. 3x
∴ D’s income = Rs. (3x – 80)
According to the question,
B : D = 1 : 2
∴ 2 (2x – 140) = 3x – 80
⇒ 4x – 280 = 3x – 80
⇒ 4x – 3x = 280 – 80
⇒ x = Rs. 200
∴ A’s income = Rs. (2 × 200) =
Rs. 400
B’s income = Rs. (400 – 140)
= Rs. 260
C’s income = Rs. (3 × 200)
= Rs. 600
D’s income = Rs. (600 – 80)
= Rs. 520Correct Option: C
Let A‘s income be Rs. 2x.
∴ B’s income = Rs. (2x – 140)
C’s income = Rs. 3x
∴ D’s income = Rs. (3x – 80)
According to the question,
B : D = 1 : 2
∴ 2 (2x – 140) = 3x – 80
⇒ 4x – 280 = 3x – 80
⇒ 4x – 3x = 280 – 80
⇒ x = Rs. 200
∴ A’s income = Rs. (2 × 200) =
Rs. 400
B’s income = Rs. (400 – 140)
= Rs. 260
C’s income = Rs. (3 × 200)
= Rs. 600
D’s income = Rs. (600 – 80)
= Rs. 520
- A man spends a part of his monthly income and saves the rest. The ratio of his expenditure to the savings is 61 : 6. If his monthly income is Rs. 8710, the amount of his monthly savings is
-
View Hint View Answer Discuss in Forum
Expenditure : Savings
= 61 : 6
Sum of the terms of ratio
= 61 + 6 = 67
Total monthly salary
= Rs. 8710
∴ Monthly savings= Rs. 
6 × 8710 
67
= Rs. 780Correct Option: D
Expenditure : Savings
= 61 : 6
Sum of the terms of ratio
= 61 + 6 = 67
Total monthly salary
= Rs. 8710
∴ Monthly savings= Rs. 
6 × 8710 
67
= Rs. 780
- A and B have their monthly incomes in the ratio 8 : 5, while their monthly expenditures are in the ratio 5 : 3. If they have saved Rs. 12,000 and Rs. 10,000 monthly respectively, then the difference in their monthly incomes is
-
View Hint View Answer Discuss in Forum
A’s monthly income = Rs. 8x
A’s monthly expenditure= Rs. 5y
B’s monthly income = Rs. 5x
B’s monthly expenditure= Rs. 3y
According to the question,
8x – 5y = 12000 ....(i)
5x – 3y = 10000 ....(ii)
By equation (i) × 3 – (ii) × 5,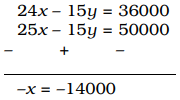
⇒ x = 14000
Difference between monthly incomes of A and B = 8x – 5x
= Rs. 3x = Rs. (3 × 14000)
= Rs. 42000Correct Option: B
A’s monthly income = Rs. 8x
A’s monthly expenditure= Rs. 5y
B’s monthly income = Rs. 5x
B’s monthly expenditure= Rs. 3y
According to the question,
8x – 5y = 12000 ....(i)
5x – 3y = 10000 ....(ii)
By equation (i) × 3 – (ii) × 5,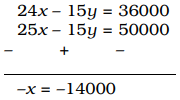
⇒ x = 14000
Difference between monthly incomes of A and B = 8x – 5x
= Rs. 3x = Rs. (3 × 14000)
= Rs. 42000
- The incomes of A and B are in the ratio 3 : 2 and their expenditures are in the ratio 5 : 3. If each saves Rs. 1000, then A’s income is
-
View Hint View Answer Discuss in Forum
Let incomes of A and B be Rs. 3x and Rs. 2x respectively. Let the expenditures of A and B be Rs. 5y and Rs. 3y respectively.
According to the question,
3x – 5y = Rs. 1000 .... (i)
2x – 3y = Rs. 1000 .... (ii)
By equation (i) × 2 – (ii) × 3,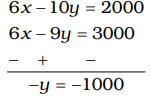
∴ y = 1000
From equation (i),
3x – 5 × 1000 = 1000
⇒ 3x = 1000 + 5000 = Rs. 6000
= A’s incomeCorrect Option: A
Let incomes of A and B be Rs. 3x and Rs. 2x respectively. Let the expenditures of A and B be Rs. 5y and Rs. 3y respectively.
According to the question,
3x – 5y = Rs. 1000 .... (i)
2x – 3y = Rs. 1000 .... (ii)
By equation (i) × 2 – (ii) × 3,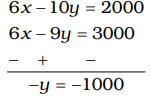
∴ y = 1000
From equation (i),
3x – 5 × 1000 = 1000
⇒ 3x = 1000 + 5000 = Rs. 6000
= A’s income
- Incomes of x and y are in the ratio 4:3. Their expenditures are in the ratio 12:7. Both save Rs. 3200 at the end of the month, then the income of x is
-
View Hint View Answer Discuss in Forum
x’s income = Rs. 4a
y’s income = Rs. 3a
x’s expenditure = Rs. 12b
y’s expenditure = Rs. 7b
∴ 4a – 12b = 3200
⇒ a – 3b = 800 ...(i)
Again, 3a – 7b = 3200 ...(ii)
By equation (i) × 7 – (ii) × 3,
⇒ a = 2000
⇒ x’s income = 4a
= 4 × 2000 = Rs. 8000Correct Option: A
x’s income = Rs. 4a
y’s income = Rs. 3a
x’s expenditure = Rs. 12b
y’s expenditure = Rs. 7b
∴ 4a – 12b = 3200
⇒ a – 3b = 800 ...(i)
Again, 3a – 7b = 3200 ...(ii)
By equation (i) × 7 – (ii) × 3,
⇒ a = 2000
⇒ x’s income = 4a
= 4 × 2000 = Rs. 8000

