Heat Transfer Miscellaneous
- A plate having 10 cm2 area each side is hanging in the middle of a room of 100 m2 total surface area. The plate temperature and emissivity are respectively 800 K and 0.6. The temperature and emissivity value for the surfaces of the room are 300 K and 0.3 respectively. Boltzmann's constant σ = 5.67 × 10-8 W/m2K4. The total heat loss from the two surfaces of the plate is
-
View Hint View Answer Discuss in Forum
Heal loss from one surface of the plate,
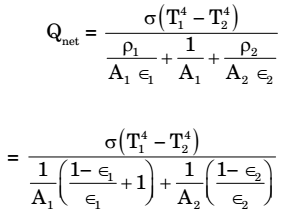
Putting A1 = 10 × 10–4 m2, T1 = 800
ε1 = 0.6 T2 = 300
A2 = 100 m2
ε2 = 0.3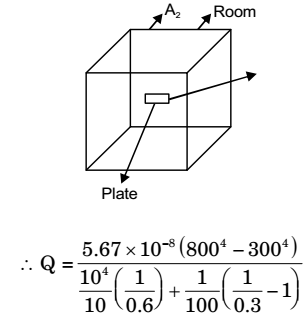
∴ Heat loss from both the surfaces
= 2 Qnet
= 2 × 13.66 = 27.32 WCorrect Option: B
Heal loss from one surface of the plate,
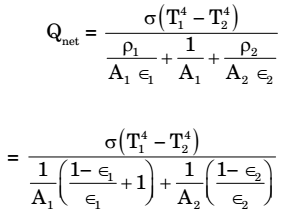
Putting A1 = 10 × 10–4 m2, T1 = 800
ε1 = 0.6 T2 = 300
A2 = 100 m2
ε2 = 0.3
∴ Heat loss from both the surfaces
= 2 Qnet
= 2 × 13.66 = 27.32 W
- A 100 W electric bulb was switched on in a 2.5 m × 3 m × 3 m size thermally insulated room having a temperature of 20°C. The room temperature at the end of 24 hours will be
-
View Hint View Answer Discuss in Forum
Heat generated by bulb = 100 × 24 × 60 × 60 Joule.
∴ Heat dissipated = ρ × V × Cv × (T – 20)
⇒ 100 × 24 × 60 × 60 = 1.24 × 9 × 2.5 × 3 × Cv (T – 20)
⇒ T = 450ºCorrect Option: D
Heat generated by bulb = 100 × 24 × 60 × 60 Joule.
∴ Heat dissipated = ρ × V × Cv × (T – 20)
⇒ 100 × 24 × 60 × 60 = 1.24 × 9 × 2.5 × 3 × Cv (T – 20)
⇒ T = 450º
Direction: Radiative heat transfer is intercepted between the inner surfaces of two very large isothermal parallel metal plates. While the upper plate (designated as plate 1) is a black surface and is the warmer one being maintained at 727°C, the lower plate (plate 2) is a diffuse and gray surface with an emissivity of 0.7 and is kept at 227°C. Assume that the surfaces are sufficiently large to form a two-surface enclosure and steady-state conditions to exist. Stefan-Boltzmann constant is given as 5.67 × 10-8W/m2K4.
- The irradiation (in kW/m2) for the plate (plate 1) is
-
View Hint View Answer Discuss in Forum
T1 = 1000 K
T2 = 500 K
ε = 0.7
Energy indicent upon plate 1 due to irradiation = Radiosity of plate 2
Energy leaving surface 2 = E2 + (1– α 2) Eb1
E2 = εσT24 = 0.7 × 5.67 × 10–8 × 5004
= 2480.62 w/m2
σ (1– α) Eb1 = Fraction of energy reflected from surface 2
= (1–0.7) × 5.67×10–8 × 10004
= 17010 w/m2
∴ Total energy incident upon plate 1 = 19.49 kW/m2Correct Option: D
T1 = 1000 K
T2 = 500 K
ε = 0.7
Energy indicent upon plate 1 due to irradiation = Radiosity of plate 2
Energy leaving surface 2 = E2 + (1– α 2) Eb1
E2 = εσT24 = 0.7 × 5.67 × 10–8 × 5004
= 2480.62 w/m2
σ (1– α) Eb1 = Fraction of energy reflected from surface 2
= (1–0.7) × 5.67×10–8 × 10004
= 17010 w/m2
∴ Total energy incident upon plate 1 = 19.49 kW/m2
- If plate 1 is also a diffuse and Gray surface with an emissivity value of 0.8, the net radiatibn heat exchange (in kW/m2) between plate 1 and plate 2 is
-
View Hint View Answer Discuss in Forum

= 0.59
∴ Q = f 12 σb (T14 – T24)
= 0.59 × 5.67 × (10000 – 625)
= 31362.18 W/m2
= 31.36 kW/m2
Alternately
1000 K = T A A (Black), εA = 0.8
500 K = TB B(Grey), εB = 0.7
Net heat exchange between A and B,Q = σ (T14 – T24) 1 + 1 - 1 εA εB = (10004 – 5004) × 5.67 × 10-8 1 + 1 - 1 0.8 0.7 = (1000)4 - (500)4 1.25 + 1.4286 - 1 = (1000)4 - (500)4 × 5.67 × 10-8 1.6786 = 53156.25 W/m2 1.6786
≈ 31.7 kW/m2Correct Option: D

= 0.59
∴ Q = f 12 σb (T14 – T24)
= 0.59 × 5.67 × (10000 – 625)
= 31362.18 W/m2
= 31.36 kW/m2
Alternately
1000 K = T A A (Black), εA = 0.8
500 K = TB B(Grey), εB = 0.7
Net heat exchange between A and B,Q = σ (T14 – T24) 1 + 1 - 1 εA εB = (10004 – 5004) × 5.67 × 10-8 1 + 1 - 1 0.8 0.7 = (1000)4 - (500)4 1.25 + 1.4286 - 1 = (1000)4 - (500)4 × 5.67 × 10-8 1.6786 = 53156.25 W/m2 1.6786
≈ 31.7 kW/m2
- Two large diffuse Gray parallel plates, separated by a small distance, have surface temperature of 400 K and 300 K. If the emissivities of the surfaces are 0.8 and the Stefan-Boltzmann constant is 5.67 × 10-8W/m2K4, the net radiation heat exchange rate in kW/m2 between the two plates is
-
View Hint View Answer Discuss in Forum
qT-2 = 0(T14 – T24) 1 + 1 - 1 ε1 ε2 = 5.67 × 10-8 (4004 - 3004) (2/8)-1
= 0.66 kW/m2Correct Option: A
qT-2 = 0(T14 – T24) 1 + 1 - 1 ε1 ε2 = 5.67 × 10-8 (4004 - 3004) (2/8)-1
= 0.66 kW/m2

