Heat Transfer Miscellaneous
- A metal ball of diameter 60 mm is initially at 220°C. The ball is suddenly cooled by an air jet of 20°C. The heat transfer coefficient is 200 W/m2K. The specific heat, thermal conductivity and density of the metal ball are 400 J/kgK, 400 W/mK and 9000 kg/m3, respectively. The ball temperature (in °C) after 90 seconds will be approximately
-
View Hint View Answer Discuss in Forum
CP = 400 J /kg-K
K = 400 W/mK
ρ = 9000 kg/m3
Time (τ) = 90 sec

hA 
τ ρVCP Ti - T∞ = e T - T∞ Put A = 3 = 100 v R 
hA 
τ = 
200 × 3 × 1 × 1 
× 90 = 0.5 ρVCP 0.03 9000 400 220 - 20 = e0.5 T - 20
By solving, we get T = 141.3°CCorrect Option: A
CP = 400 J /kg-K
K = 400 W/mK
ρ = 9000 kg/m3
Time (τ) = 90 sec

hA 
τ ρVCP Ti - T∞ = e T - T∞ Put A = 3 = 100 v R 
hA 
τ = 
200 × 3 × 1 × 1 
× 90 = 0.5 ρVCP 0.03 9000 400 220 - 20 = e0.5 T - 20
By solving, we get T = 141.3°C
- A brick wall (k = 0.9 W/mK) of thickness 0.18 m separates the warm air in a room from the cold ambient air. On a particular Winter day, the outside air temperature is - 5°C and the room needs to be maintained at 27°C. The heat transfer coefficient associated with outside air is 20 W/m2K. Neglecting the convective resistance of the air inside the room, the heat loss, in (W/m2), is
-
View Hint View Answer Discuss in Forum

Total thermal resistance1 = 1 Rth 1 + 1 h k 1 = 1 = 4 w/m2K Rth 1 + 0.18 20 0.9 Q = ∆T [27 - (-5)] × 4 = 128 W/m2 Rth Correct Option: C

Total thermal resistance1 = 1 Rth 1 + 1 h k 1 = 1 = 4 w/m2K Rth 1 + 0.18 20 0.9 Q = ∆T [27 - (-5)] × 4 = 128 W/m2 Rth
- A plastic sleeve of outer radius r0 = 1 mm covers a wire (radius r = 0.5 mm) carrying electric current, Thermal conductivity of the plastic is 0.12 W/mK. The heat transfer coefficient on the outer surface of the sleeve exposed to air is 25 W/m2K. Due to the addition of the plastic cover, the heat transfer from the wire to the ambient will
-
View Hint View Answer Discuss in Forum
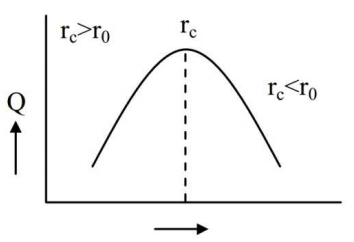
r0 = 1 mm, k = 0.15 W/m-k
h = 25 W/m2 -Krc = k for cylindrical shape h0 = 0.15 × 1000 = 0.15 × 40 = 6mm 25
∴ rc > r0
⇒ The heat transfer from the wire to the ambient will increaseCorrect Option: A

r0 = 1 mm, k = 0.15 W/m-k
h = 25 W/m2 -Krc = k for cylindrical shape h0 = 0.15 × 1000 = 0.15 × 40 = 6mm 25
∴ rc > r0
⇒ The heat transfer from the wire to the ambient will increase
- Steady one-dimensional heat conduction takes place across the faces 1 and 3 of a composite slab consisting of slabs A and B in perfect contact as shown in the figure, where kA, kB denote the respective thermal conductivities. Using the data as given in the figure, the interface temperature T2 (in °C) is _________

-
View Hint View Answer Discuss in Forum
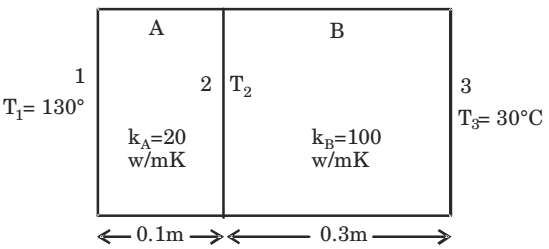
Q = kA.(T1 - T2) A LA = kB(T2 - T3) LB 20(130 - T2) = 100(T2 - 30) 0.1 0.3
∴ T2 = 67.5°CCorrect Option: A

Q = kA.(T1 - T2) A LA = kB(T2 - T3) LB 20(130 - T2) = 100(T2 - 30) 0.1 0.3
∴ T2 = 67.5°C
- One-dimensional steady state heat conduction takes place through a sol i d whose cross sectional area varies linearly in the direction of heat transfer. Assume t her e is no heat generation in the solid and the thermal conductivity of the material is constant and independent of temperature. The temperature distribution in the solid is
-
View Hint View Answer Discuss in Forum
We know that one-dimensional steady state heat conduction equation with no heat generation is given by,
d 
- kA dT 
= 0 dx dx ⇒ -kA dT = C1 dx
∵ A = Cx + B (linear variation)
Logarithmic temperature distributionCorrect Option: C
We know that one-dimensional steady state heat conduction equation with no heat generation is given by,
d 
- kA dT 
= 0 dx dx ⇒ -kA dT = C1 dx
∵ A = Cx + B (linear variation)
Logarithmic temperature distribution

