101. For the three-dimensional object shown in the figure below, five faces are insulated. The sixth face (PQRS), which is not insulated, interacts thermally with the ambient, with a convective heat transfer coefficient of 10W/m²K. The ambient temperature is 30°C. Heat is uniformly generated inside the object at the rate of 100 W/m³. Assuming the face PQRS to be at uniform temperature, its steady state temperature is
     

1. 1. 10°C

   
   
   

   2. 20°C

   
   
   

   3. 30°C

   
   
   

   4. 40°C

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given data;
   h_o = W/m²K
   h_o = 30 °C
   q_G = 100 W/m³
   Volume, V = 2×1×2=4 m³
   
   Heat generated, Q = q_G × V = 100 × 4 = 400 W
   Convection heat transfer from face PQRS,
   Q = h_o A (T_s – T_o)
   400 = 10 × 2 × 2 (T_s – 30)
   T_s = 40°C

   Correct Option: D

   Given data;
   h_o = W/m²K
   h_o = 30 °C
   q_G = 100 W/m³
   Volume, V = 2×1×2=4 m³
   
   Heat generated, Q = q_G × V = 100 × 4 = 400 W
   Convection heat transfer from face PQRS,
   Q = h_o A (T_s – T_o)
   400 = 10 × 2 × 2 (T_s – 30)
   T_s = 40°C

---

102. A stainless steel tube (k_s = 19 W/mK) of 2 cm ID and 5 cm OD is insulated with 3 cm thick asbestos (k_a = 0.2 W/mK). If the temperature difference between the inner most and outermost surfaces is 600°C, the heat transfer rate per unit length is

1. 1. 0.94 W/m

   
   
   

   2. 9.44 W/m

   
   
   

   3. 944.72 W/m

   
   
   

   4. 9447.21 W/m

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given: d₁ = 2 cm
   r₁ = 1 cm
   d₂ = 5 cm
   r₂ = 2.5 cm
   d₃ = 5 + 2 × 3 = 11
   r₃ = 5.5 cm
   Equivalent thermal resistance
   
   

   Rt =	1	In	r2	+	1	In	r3
   	2πkst		r1		2πka		r2

   
   

   =	1	In	2.5	+	1	In	5.5
   	2π × 19		1		2π × 0.2		2.5

   
   = 7.67 × 10^–3 + 0.627 = 0.635
   ∴ Heat transfer rate per unit length
   

   	t1 - t2	=	600	= 944.88 W/m
   	Rt		0.635

   Correct Option: C

   Given: d₁ = 2 cm
   r₁ = 1 cm
   d₂ = 5 cm
   r₂ = 2.5 cm
   d₃ = 5 + 2 × 3 = 11
   r₃ = 5.5 cm
   Equivalent thermal resistance
   
   

   Rt =	1	In	r2	+	1	In	r3
   	2πkst		r1		2πka		r2

   
   

   =	1	In	2.5	+	1	In	5.5
   	2π × 19		1		2π × 0.2		2.5

   
   = 7.67 × 10^–3 + 0.627 = 0.635
   ∴ Heat transfer rate per unit length
   

   	t1 - t2	=	600	= 944.88 W/m
   	Rt		0.635

---

---

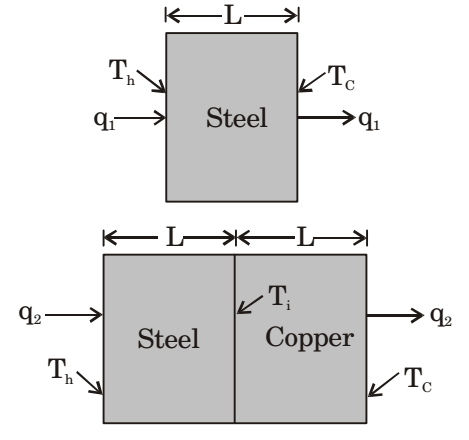
103. A well machined steel plate of thickness L is kept such that the wall temperature are Th and Tc as seen in the figure below. A smooth copper plate of the same thickness L is now attached to the steel plate without any gap as indicated in the figure below. The temperature at the interface is T_t. The temperatures of the outer walls are still the same at T_h and T_c. The heat transfer rates are q₁ and q₂ per unit area in the two cases respectively in the direction shown. Which of the following statements is correct?
     

1. 1. T_h > T_i > T_c and q₁ < q₂

   
   
   

   2. T_h < T_i > T_c and q₁ = q₂

   
   
   

   3. T_h = (T_i + T_c )/2 and q₁ > q₂

   
   
   

   4. T_i < (T_h + T_c )/2 and q₁ > q₂

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
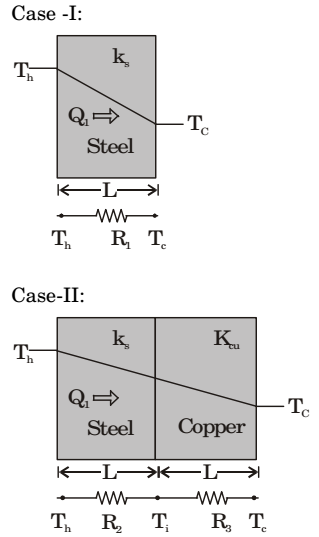
   For caseI-:
   

   Q1 =	Th - Tc
   	R1

   
   

   where R1 =	L
   	KSA

   
   For Case-II:
   

   Q2 =	Th - Tc
   	R2 + R3

   
   

   where R2 =	L	and R3 =	L
   	KsA		KcuA

   
   As R₂ + R₃ > R₁ at constant temperature difference in both cases.
   

   Then q1		or	Q1		> q2		or	Q2
   			A					A

   
   For Case-II:
   R₂ > R₃
   ∵ k_cu > k_s
   

   Q2 =	Th - T1
   	R2

   
   

   or R2 =	Th - T1
   	Q2

   
   

   also Q2 =	Ti - Tc
   	R3

   
   

   or R3 =	Ti - Tc
   	Q2

   
   

   ∴	Th - Ti	>	Ti - Tc
   	Q2		Q2

   
   or T_h – T_i > T_i – T_c
   or T_h + T_c > 2T_i
   

   or Ti <	Th + Tc
   	2

   Correct Option: D

   
   For caseI-:
   

   Q1 =	Th - Tc
   	R1

   
   

   where R1 =	L
   	KSA

   
   For Case-II:
   

   Q2 =	Th - Tc
   	R2 + R3

   
   

   where R2 =	L	and R3 =	L
   	KsA		KcuA

   
   As R₂ + R₃ > R₁ at constant temperature difference in both cases.
   

   Then q1		or	Q1		> q2		or	Q2
   			A					A

   
   For Case-II:
   R₂ > R₃
   ∵ k_cu > k_s
   

   Q2 =	Th - T1
   	R2

   
   

   or R2 =	Th - T1
   	Q2

   
   

   also Q2 =	Ti - Tc
   	R3

   
   

   or R3 =	Ti - Tc
   	Q2

   
   

   ∴	Th - Ti	>	Ti - Tc
   	Q2		Q2

   
   or T_h – T_i > T_i – T_c
   or T_h + T_c > 2T_i
   

   or Ti <	Th + Tc
   	2

---

104. In a case of one dimensional heat conduction in a medium with constant properties, T is the temperature at position x, at time t.
     

     Then	δT	is proportional to
     	δt

1. 1. T

      x

   
   
   

   2. δT

      δx

   
   
   

   3. δ2T

      δxδt

   
   
   

   4. δ2T

      δx2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   One dimensional heat conduction equation is,
   

   	δ2T	=	1		δT
   	δx2		α		δt

   
   

   ∴	δ2T	∝	δT
   	δx2		δt

   Correct Option: D

   One dimensional heat conduction equation is,
   

   	δ2T	=	1		δT
   	δx2		α		δt

   
   

   ∴	δ2T	∝	δT
   	δx2		δt

---

---

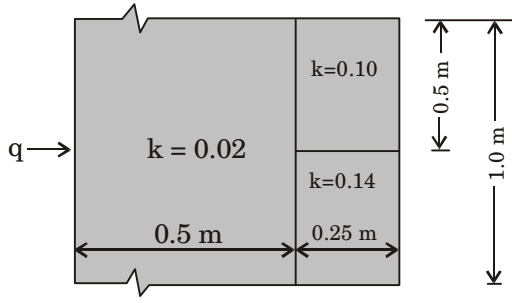
105. Heat flows through a composite slab, as shown below. The depth of the slab is 1 m. The k values are in W/mK. The overall thermal resistance in K/W is
     

1. 1. 17.2

   
   
   

   2. 21.9

   
   
   

   3. 28.6

   
   
   

   4. 39.2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   	L1	=	0.5	= 25
   	k1		0.02

   
   

   	2L2	= 5
   	k2

   
   

   	2L3	= 12.5
   	k3

   
   R_total = 25 + 3.6 = 28.6 K/W

   Correct Option: C

   	L1	=	0.5	= 25
   	k1		0.02

   
   

   	2L2	= 5
   	k2

   
   

   	2L3	= 12.5
   	k3

   
   R_total = 25 + 3.6 = 28.6 K/W

---