96. Consider one dimensional steady state heat conduction across a wall (as shown in figure below) of thickness 30 mm and thermal conductivity 15 W/mK. At x = 0, a constant heat flux, q'' = 1 × 10⁵ W/m² is applied. On the other side of the wall, heat is removed from the wall by convection with a fluid at 25°C and heat transfer coefficient of 250 W/m²K. The temperature (in °C), at x = 0 is _______.
    
    

1. 1. 625°

   
   
   

   2. 626°

   
   
   

   3. 624°

   
   
   

   4. 632°

   
   
   

---

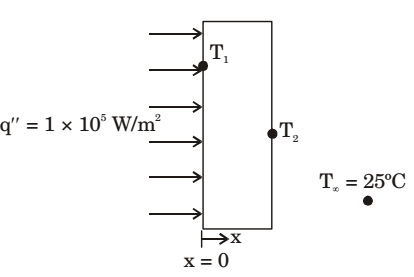
1. View Hint View Answer Discuss in Forum

   

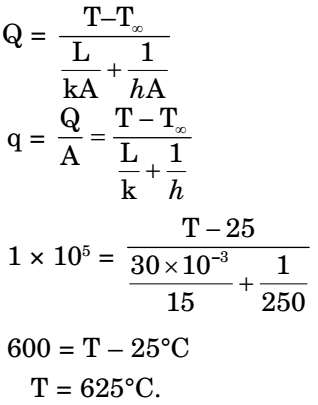
   Correct Option: A

   

---

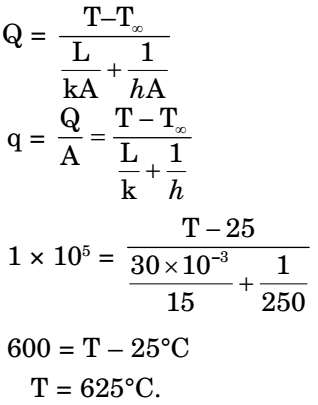
97. A material P of thickness 1 mm is sandwiched between two steel slabs, as shown in the figure below. A heat flux 10 kW/m² is supplied to one of the steel slabs as shown. The boundary temperatures of the slabs are indicated in the figure. Assume thermal conductivity of this steel is 10 W/mK. Considering one-dimensional steady state heat conduction for the configuration, the thermal conductivity (k, inW/mK) of material P is ________.
    

1. 1. 0.10 W/m.k.

   
   
   

   2. 1.10 W/m.k.

   
   
   

   3. -0.10 W/m.k.

   
   
   

   4. -1.10 W/m.k.

   
   
   

---

1. View Hint View Answer Discuss in Forum

   

   Correct Option: A

   

---

---

98. A plane wall has a thermal conductivity of 1.15 W/mK. If the inner surface is at 1100°C and the outer surface is at 350°C, then the design thickness (in meter) of the wall to maintain a steady heat flux of 2500 W/m² should be

1. 1. 0.345 m.

   
   
   

   2. 0.245 m.

   
   
   

   3. 1.145 m.

   
   
   

   4. 1.345 m.

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Q = KA	dt
   	dx

   
   

   q =	Q	= 2500 W/m²
   	A

   
   

   2500 = K	6dt
   	dx

   
   

   2500 = 1.15 × =	(1100 - 350)
   	x

   
   x = 0.345 m.

   Correct Option: A

   Q = KA	dt
   	dx

   
   

   q =	Q	= 2500 W/m²
   	A

   
   

   2500 = K	6dt
   	dx

   
   

   2500 = 1.15 × =	(1100 - 350)
   	x

   
   x = 0.345 m.

---

99. A cylindrical uranium fuel rod of radius 5 mm in a nuclear is generating heat at the rate of 4 × 107 W/m³. The rod is cooled by a liquid (convective heat transfer coefficient 1000 W/ m²K) at 25°C. At steady state, the surface temperature (in K) of the rod is

1. 1. 308

   
   
   

   2. 398

   
   
   

   3. 418

   
   
   

   4. 448

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given data: r = 0.005 m
   d = 2r = 2 × 0.005 = 0.010 m
   

   q6 = 4 × 107	W
   	m3

   
   

   h0 = 1000	W
   	m2K

   
   T₀ = 25°c
   For steady state,
   Rate of heat generation in the rod} = Rate of convection H.T. from rod surface to fluid q_G × volume of rod = h₀ A(T_s – T₀)
   

   qG ×	π	d²l = h0 × πdl (Ts - T0)
   	4

   
   

   d.qG (Ts - T0)

   = h0

   4

   
   

   h0	.010 × 4 × 107	= 1000 (Ts - 25)
   	m24

   
   T_s – 25 = 100
   T_s = 125° c or 398 K

   Correct Option: B

   Given data: r = 0.005 m
   d = 2r = 2 × 0.005 = 0.010 m
   

   q6 = 4 × 107	W
   	m3

   
   

   h0 = 1000	W
   	m2K

   
   T₀ = 25°c
   For steady state,
   Rate of heat generation in the rod} = Rate of convection H.T. from rod surface to fluid q_G × volume of rod = h₀ A(T_s – T₀)
   

   qG ×	π	d²l = h0 × πdl (Ts - T0)
   	4

   
   

   d.qG (Ts - T0)

   = h0

   4

   
   

   h0	.010 × 4 × 107	= 1000 (Ts - 25)
   	m24

   
   T_s – 25 = 100
   T_s = 125° c or 398 K

---

---

100. Heat is generated uniformly in a long solid cylindrical rod (diameter =10 mm) at the rate of 4 × 10⁷ W/m³. The thermal conductivity of the rod material is 25 W/mK. Under steady state conditions, the temperature ditference between the centre and the surface of the rod is 1°C.

1. 1. -10°C

   
   
   

   2. 10°C

   
   
   

   3. -11°C

   
   
   

   4. -9°C

   
   
   

---

1. View Hint View Answer Discuss in Forum

   

   Correct Option: A

   

---