106. In a composite slab, the temperature at the interface (T_inter) between two materials is equal to the average of the temperature at the two ends. Assuming steady one dimensional heat conduction, which of the following statements is true about the respective thermal conductivity?
     

1. 1. 2k₁ = k₂

   
   
   

   2. k₁ = k₂

   
   
   

   3. 2k₁ = 3k₂

   
   
   

   4. k₁ = 2k₂

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Q =	-k1A	(Tinter - T1) =	-k2A(T2 - Tinter)
   	2b		b

   
   

   Tinter =	T1 + T2
   	2

   
   ∴ k₁ = 2k₂

   Correct Option: D

   Q =	-k1A	(Tinter - T1) =	-k2A(T2 - Tinter)
   	2b		b

   
   

   Tinter =	T1 + T2
   	2

   
   ∴ k₁ = 2k₂

---

107. Heat is being transferred conductivity from a cylindrical nuclear reactor fuel rod of 50 mm diameter to water at 75°C, under steady state condition, the rate of heat generation within the fuel element is 106 W/m³ and the convective heat transfer coefficient is 1 kW/m²K, the outer surface temperature of the fuel element would be

1. 1. 700 K

   
   
   

   2. 625 K

   
   
   

   3. 360 K

   
   
   

   4. 400 K

   
   
   

---

1. View Hint View Answer Discuss in Forum

   By applying energy balance, we get
   Rate of heat generation = Rate of convective heat transfer
   q_G × Volume of fuel rod = h₀ A (T_s – T₀)
   

   qQ ×	π	d2 × 1 = h0 × πdl(Ts – T0)
   	4

   
   

   	d.qQ	= h0(Ts – T0)
   	4

   
   

   	0.05 × 1 × 103	(Ts – 75)
   	4

   
   T_s – 75 = 12.5
   T_s = 87.5°C or 360.5K

   Correct Option: C

   By applying energy balance, we get
   Rate of heat generation = Rate of convective heat transfer
   q_G × Volume of fuel rod = h₀ A (T_s – T₀)
   

   qQ ×	π	d2 × 1 = h0 × πdl(Ts – T0)
   	4

   
   

   	d.qQ	= h0(Ts – T0)
   	4

   
   

   	0.05 × 1 × 103	(Ts – 75)
   	4

   
   T_s – 75 = 12.5
   T_s = 87.5°C or 360.5K

---

---

108. Steady two-dimensional heat conduction takes place in the body shown in the figure below. The normal temperature gradients over surface P and Q can be considered to be uniform. The temperature gradient δT/δt at surface Q is equal to 10 K/m. Surfaces P and Q are maintained at constant temperatures as shown in the figure, while the remaining part of the boundary is insulated. The body has a constant thermal conductivity of 0.1 W/mK.
     

     The values of	δT	and	δT	at surface P are
     	δy		δx

     
     

1. 1. 	δT	= 20 K/m	δT	= 0 K/m
      	δx		δy

   
   
   

   2. 	δT	= 0 K/m	δT	= 10 K/m
      	δx		δy

   
   
   

   3. 	δT	= 10 K/m	δT	= 10 K/m
      	δx		δy

   
   
   

   4. 	δT	= 0 K/m	δT	= 20 K/m
      	δx		δy

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Direction of heat flow is always normal to surface of constant temperature
   So for surface P₁, dT/dx = 0
   From energy conservation,
   Heat rate at P = Heat rate at Q
   

   0.1 × 1

   dT

   = 0.1 × 2 ×

   dT

   dy

   P

   dx

   Q

   
   

   ⇒	dT	= 20 K/m
   	dy

   Correct Option: D

   Direction of heat flow is always normal to surface of constant temperature
   So for surface P₁, dT/dx = 0
   From energy conservation,
   Heat rate at P = Heat rate at Q
   

   0.1 × 1

   dT

   = 0.1 × 2 ×

   dT

   dy

   P

   dx

   Q

   
   

   ⇒	dT	= 20 K/m
   	dy

---

109. Heat transfer through a composite wall is shown in figure. Both the sections of the wall have equal thickness (/). The conductivity of one section is k and that of the other is 2k. The left face of the wall is at 600 K and the right face is at 300 K.
     
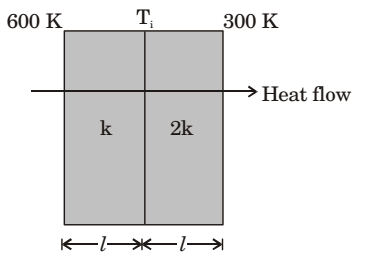
     The interface temperature T_i (in K) of the composite wall is __________

1. 1. 400 K

   
   
   

   2. 600 K

   
   
   

   3. 700 K

   
   
   

   4. 800 K

   
   
   

---

1. View Hint View Answer Discuss in Forum

   R = R₁ + R₂
   

   =	L	+	L	=	L	+	L	=	3L
   	KA		KA		KA		2KA		2KA

   
   

   Q =	TL - TR
   	TR

   
   

   =	300	= 200 ×	KA
   	3L		L
   	2KA

   
   At interface,
   

   Q =	TL - Ti
   	Ti

   
   

   =	600 - Ti	= (600 - Ti)	KA
   	L		L
   	KA

   
   

   200	KA	= (600 - Ti)	KA
   	L		L

   
   200 = 600 – T_i
   T_i = 400 K

   Correct Option: A

   R = R₁ + R₂
   

   =	L	+	L	=	L	+	L	=	3L
   	KA		KA		KA		2KA		2KA

   
   

   Q =	TL - TR
   	TR

   
   

   =	300	= 200 ×	KA
   	3L		L
   	2KA

   
   At interface,
   

   Q =	TL - Ti
   	Ti

   
   

   =	600 - Ti	= (600 - Ti)	KA
   	L		L
   	KA

   
   

   200	KA	= (600 - Ti)	KA
   	L		L

   
   200 = 600 – T_i
   T_i = 400 K

---

---

110. In pool boiling the highest HTC occurs in

1. 1. Sub cooled boiling zone

   
   
   

   2. Nucleate boiling zone

   
   
   

   3. Partial film boiling zone

   
   
   

   4. Film boiling zone

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Nucleate boiling zone

   Correct Option: B

   Nucleate boiling zone

---